题目内容
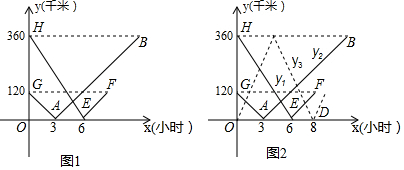
5. 如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).
如图,⊙M的圆心M(-1,2),⊙M经过坐标原点O,与y轴交于点A.经过点A的一条直线l解析式为:y=-$\frac{1}{2}$x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(-4,0).(1)求抛物线的解析式;
(2)求证:直线l是⊙M的切线;
(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E;PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小.若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.
分析 (1)设抛物线的解析式为y=a(x-2)(x+4),将点M的坐标代入可求得a的值,从而得到抛物线的解析式;
(2)连接AM,过点M作MG⊥AD,垂足为G.先求得点A和点B的坐标,可求得,可得到AG、ME、OA、OB的长,然后利用锐角三角函数的定义可证明∠MAG=∠ABD,故此可证明AM⊥AB;
(3))先证明∠FPE=∠FBD.则PF:PE:EF=$\sqrt{5}$:2:1.则△PEF的面积=$\frac{1}{5}$PF2,设点P的坐标为(x,-$\frac{2}{9}$x2-$\frac{4}{9}$x+$\frac{16}{9}$),则F(x,-$\frac{1}{2}$x+4).然后可得到PF与x的函数关系式,最后利用二次函数的性质求解即可.
解答 解:(1)设抛物线的解析式为y=a(x-2)(x+4),将点M的坐标代入得:-9a=2,解得:a=-$\frac{2}{9}$.
∴抛物线的解析式为y=-$\frac{2}{9}$x2-$\frac{4}{9}$x+$\frac{16}{9}$.
(2)连接AM,过点M作MG⊥AD,垂足为G.
把x=0代入y=-$\frac{1}{2}$x+4得:y=4,
∴A(0,4).
将y=0代入得:0=-$\frac{1}{2}$x+4,解得x=8,
∴B(8,0).
∴OA=4,OB=8.
∵M(-1,2),A(0,4),
∴MG=1,AG=2.
∴tan∠MAG=tan∠ABO=$\frac{1}{2}$.
∴∠MAG=∠ABO.
∵∠OAB+∠ABO=90°,
∴∠MAG+∠OAB=90°,即∠MAB=90°.
∴l是⊙M的切线.
(3)∵∠PFE+∠FPE=90°,∠FBD+∠PFE=90°,
∴∠FPE=∠FBD.
∴tan∠FPE=$\frac{1}{2}$.
∴PF:PE:EF=$\sqrt{5}$:2:1.
∴△PEF的面积=$\frac{1}{2}$PE•EF=$\frac{1}{2}$×$\frac{2\sqrt{5}}{5}$PF•$\frac{\sqrt{5}}{5}$PF=$\frac{1}{5}$PF2.
∴当PF最小时,△PEF的面积最小.
设点P的坐标为(x,-$\frac{2}{9}$x2-$\frac{4}{9}$x+$\frac{16}{9}$),则F(x,-$\frac{1}{2}$x+4).
∴PF=(-$\frac{1}{2}$x+4)-(-$\frac{2}{9}$x2-$\frac{4}{9}$x+$\frac{16}{9}$)=-$\frac{1}{2}$x+4+$\frac{2}{9}$x2+$\frac{4}{9}$x-$\frac{16}{9}$=$\frac{2}{9}$x2-$\frac{1}{18}$x+$\frac{20}{9}$=$\frac{2}{9}$(x-$\frac{1}{8}$)2+$\frac{71}{32}$.
∴当x=$\frac{1}{8}$时,PF有最小值,PF的最小值为$\frac{71}{32}$.
∴P($\frac{1}{8}$,$\frac{55}{32}$).
∴△PEF的面积的最小值为=$\frac{1}{5}$×($\frac{71}{32}$)2=$\frac{5041}{5120}$.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用待定系数法求二次函数的解析式、二次函数的性质、锐角三角函数的定义,列出PF与x的函数关系式是解题的关键.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案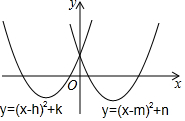 图中是有相同最小值的两条抛物线,则下列关系中正确的是( )
图中是有相同最小值的两条抛物线,则下列关系中正确的是( )| A. | k<n | B. | h=m | C. | k+n=0 | D. | h<0,m>0 |
| A. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ |
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 5 | 7 |
| A. | 15,14 | B. | 15,15 | C. | 16,14 | D. | 16,15 |
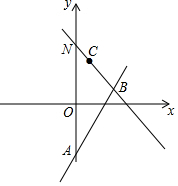 如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,点直线y=-x+5交于点B(4,n),C为直线y=-x+5上任意一点
如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,点直线y=-x+5交于点B(4,n),C为直线y=-x+5上任意一点