题目内容
17.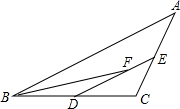 在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用中位线定理,得到DE∥AB,根据平行线的性质,可得∠EDC=∠ABC,再利用角平分线的性质和三角形内角外角的关系,得到DF=DB,进而求出DF的长,易求EF的长度.
解答 解:∵在△ABC中,D、E分别是BC、AC的中点,AB=8,
∴DE∥AB,DE=$\frac{1}{2}$AB=4.
∴∠EDC=∠ABC.
∵BF平分∠ABC,
∴∠EDC=2∠FBD.
∵在△BDF中,∠EDC=∠FBD+∠BFD,
∴∠DBF=∠DFB,
∴FD=BD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3.
∴FE=DE-DF=4-3=1.
故选:A.
点评 本题考查了三角形中位线定理和等腰三角形的判定于性质.三角形的中位线平行于第三边,当出现角平分线,平行线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
5.下列方程中,是二元一次方程的是( )
| A. | x=1-2y | B. | $\frac{1}{x}$=1-2y | C. | x2=1-2y | D. | x=z-2y |
6.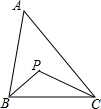 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )| A. | 80 | B. | 110 | C. | 130 | D. | 140 |
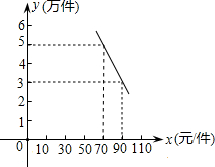 某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.
某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.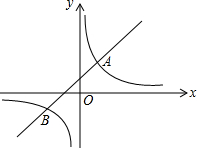 如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.
如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.