题目内容
15.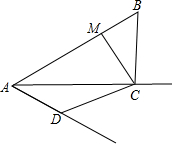 如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
如图,AC平分∠BAD,CM⊥AB于M,且AB+AD=2AM,试求∠ADC+∠ABC的度数.
分析 在AB上截取AE=AD,连接CE,作CN⊥AD于N,由角平分线的性质得出CM=CN,再证明△ACE≌△ACD,得出CE=CD,证出CB=CD,然后由HL证明Rt△CDN≌△RtCBM,得出对应角相等∠CDN=∠B,运用平角的定义即可得出结果.
解答 解:在AB上截取AE=AD,连接CE,作CN⊥AD于N,如图所示: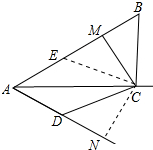 ∵AC平分∠BAD,CM⊥AB于M,
∵AC平分∠BAD,CM⊥AB于M,
∴∠EAC=∠DAC,CM=CN,
在△ACE和△ACD中,
$\left\{\begin{array}{l}{AE=AD}&{\;}\\{∠EAC=∠DAC}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ACE≌△ACD(SAS),
∴CE=CD,
∵AB+AD=2AM,
∴AE+BE+AD=2(AE+EM),
∴BE=2EM,
∴EM=BM,
∵CM⊥AB,
∴CB=CE,
∴CB=CD,
在Rt△CDN和△RtCBM中,
$\left\{\begin{array}{l}{CD=CB}&{\;}\\{CN=CM}&{\;}\end{array}\right.$,
∴Rt△CDN≌△RtCBM(HL),
∴∠CDN=∠B,
∵∠ADC+∠CDN=180°,
∴∠ADC+∠B=180°.
点评 本题考查了角平分线的性质、全等三角形的判定与性质、线段垂直平分线的性质、平角的定义;本题有一定难度,需要通过作辅助线构造三角形全等才能得出结果.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
5.下列方程中,是二元一次方程的是( )
| A. | x=1-2y | B. | $\frac{1}{x}$=1-2y | C. | x2=1-2y | D. | x=z-2y |
6.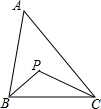 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )| A. | 80 | B. | 110 | C. | 130 | D. | 140 |
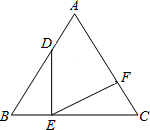 如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,AD=BE,∠DEF=60°,说明AD=CF.
如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,AD=BE,∠DEF=60°,说明AD=CF.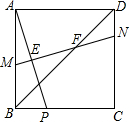 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.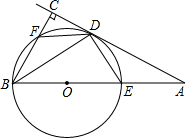 如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.
如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.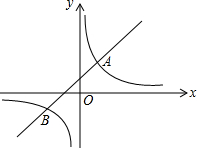 如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.
如图,直线y=k1+b与双曲线y=$\frac{{k}_{2}}{x}$相交于A(m,2),B(-2,-1)两点.则不等式k1x+b>$\frac{{k}_{2}}{x}$的解集为x>1或-2<x<0.