题目内容
1.已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中A(1,0),B(3,0),C(0,-3).(1)求抛物线的解析式;
(2)若点P在抛物线上运动(点P异于点A),
①当△PBC的面积与△ABC的面积相等时,求点P的坐标;
②如图2,当∠PCB=∠BCA时,求直线CP的解析式.
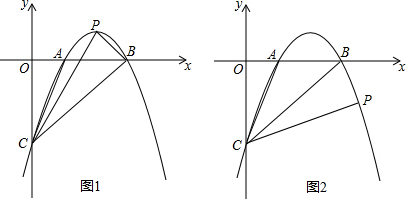
分析 (1)根据对称轴公式,A、C两点坐标,列方程组,求抛物线解析式;
(2)①只需要AP∥BC即可满足题意,先求直线BC解析式,根据平行线的解析式一次项系数相等,设直线AP的解析式,将A点坐标代入可求直线AP的解析式,将抛物线与直线AP解析式联立,即可求P点坐标,再根据平移法求满足条件的另外两个P点坐标;
②延长CP交x轴于点Q,根据抛物线解析式可知△OBC为等腰直角三角形,利用角的关系证明∠OCA=∠OQC,可证Rt△AOC∽Rt△COQ,利用相似比求解.
解答 解:(1)由题意,得:
$\left\{\begin{array}{l}{a+b+c=0}\\{c=-3}\\{-\frac{b}{2a}=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=-3}\end{array}\right.$.
故抛物线的解析式为y=-x2+4x-3;
(2)①当点P在x轴上方时,如图1,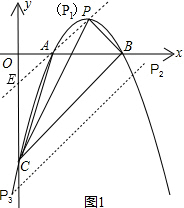
过点A作直线BC的平行线交抛物线于点P,
设BC所在直线解析式为:y=kx+d,
则$\left\{\begin{array}{l}{3k+d=0}\\{d=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{d=-3}\\{k=1}\end{array}\right.$
故直线BC的解析式为y=x-3,
设直线AP的解析式为y=x+n,
∵直线AP过点A(1,0),代入求得n=-1.
∴直线AP的解析式为y=x-1
解方程组$\left\{\begin{array}{l}{y=x-1}\\{y=-{x}^{2}+4x-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=0}\end{array}\right.$,
∴点P1(2,1),
当点P在x轴下方时,如图1:
设直线AP1交y轴于点E(0,-1),
把直线BC向下平移2个单位,交抛物线于点P2,P3,
得直线P2P3的解析式为y=x-5,
解方程组$\left\{\begin{array}{l}{y=x-5}\\{y=-{x}^{2}+4x-3}\end{array}\right.$,
得$\left\{\begin{array}{l}{{x}_{1}=\frac{3+\sqrt{17}}{2}}\\{{y}_{1}=\frac{-7+\sqrt{17}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{3-\sqrt{17}}{2}}\\{{y}_{2}=\frac{-7-\sqrt{17}}{2}}\end{array}\right.$,
∴P2($\frac{3+\sqrt{17}}{2}$,$\frac{-7+\sqrt{17}}{2}$),P3($\frac{3-\sqrt{17}}{2}$,$\frac{-7-\sqrt{17}}{2}$),
综上所述,点P的坐标为:P1(2,1),P2($\frac{3+\sqrt{17}}{2}$,$\frac{-7+\sqrt{17}}{2}$),P3($\frac{3-\sqrt{17}}{2}$,$\frac{-7-\sqrt{17}}{2}$);
②∵B(3,0),C(0,-3),
∴OB=OC,
∴∠OCB=∠OBC=45°,
设直线CP的解析式为y=wx-3,
如图2,延长CP交x轴于点Q,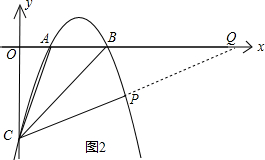
设∠OCA=α,则∠ACB=45°-α,
∵∠PCB=∠BCA,
∴∠PCB=45°-α,
∴∠OQC=∠OBC-∠PCB=45°-(45°-α)=α,
∴∠OCA=∠OQC,
又∵∠AOC=∠COQ=90°,
∴Rt△AOC∽Rt△COQ,
∴$\frac{OA}{OC}$=$\frac{OC}{OQ}$,
∴$\frac{1}{3}$=$\frac{3}{OQ}$,
∴OQ=9,∴Q(9,0)
∵直线CP过点Q(9,0),
∴9w-3=0,
∴w=$\frac{1}{3}$.
∴直线CP的解析式为:y=$\frac{1}{3}$x-3.
点评 此题主要考查了二次函数的综合题型,其中涉及到的知识点有运用待定系数法求一次函数、二次函数的解析式,三角形的面积,两函数交点坐标的求法,相似三角形的判定与性质,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.

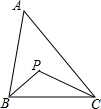 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )| A. | 80 | B. | 110 | C. | 130 | D. | 140 |
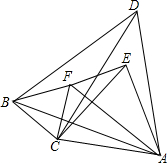 如图所示,平面上三个正三角形ACE,△ABD,△BCF两两共有一个顶点,求证:CD与EF互相平分.
如图所示,平面上三个正三角形ACE,△ABD,△BCF两两共有一个顶点,求证:CD与EF互相平分.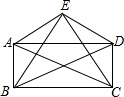 如图,平行四边形ABCD中,以对角线AC为斜边作Rt△ACE,又∠BED=90°,那么平行四边形ABCD是矩形吗?说说你的理由.
如图,平行四边形ABCD中,以对角线AC为斜边作Rt△ACE,又∠BED=90°,那么平行四边形ABCD是矩形吗?说说你的理由.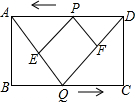 如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.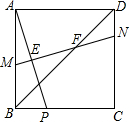 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.