题目内容
2.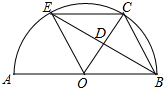 如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.
如图,AB是半圆O的直径,点C是半圆O上一点,∠COB=60°,点D是OC的中点,连接BD,BD的延长线交半圆O于点E,连接OE,EC,BC.(1)求证:△BDO≌△EDC.
(2)若OB=6,则四边形OBCE的面积为18$\sqrt{3}$.
分析 (1)证明方法比较多,根据全等三角形判定方法判定即可.
(2)先证明四边形OBCE是菱形,求出对角线的长即可求面积.
解答 (1)证明:∵∠COB=60°且OB=OC,
∴△BOC为等边三角形,∠OBC=60°,
又∵点D是OC的中点,
∴OD=CD,∠OBD=$\frac{1}{2}∠OBC$=30°,
又∵点C是半圆上一点且∠COB=60°,
∴∠CEB=$\frac{1}{2}∠COB$=30°,
∴∠OBD=∠CEB,
在△BDO与△EDC中,
$\left\{\begin{array}{l}{∠OBD=∠CED}\\{∠BDO=∠EDC}\\{OD=CD}\end{array}\right.$,
∴△BDO≌△EDC(AAS);
(2)∵∴△BDO≌△EDC,
∴EC=OB,
∵△OBC是等边三角形,
∴OB=BC=EC=EO,
∴四边形OBCE是菱形,
∴S菱形OBCE=$\frac{1}{2}$•OC•EB=$\frac{1}{2}$•6•6$\sqrt{3}$=18$\sqrt{3}$.
点评 本题考查全等三角形的判定和性质、菱形的判定和性质、菱形的面积,解题的关键是熟练掌握全等三角形的判定,记住菱形的面积等于对角线乘积的一半,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
 如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )
如图,E是?ABCD内任一点,若S?ABCD=8,则阴影部分的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A(-2,1),则当x<-1时,函数值y的取值范围是( )
| A. | y>2 | B. | -2<y<0 | C. | y>-2 | D. | 0<y<2 |
11.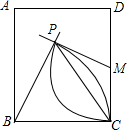 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
 如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )
如图,矩形ABCD中,M为CD中点,分别以B、M为圆心,以BC长、MC长为半径画弧,两弧相交于点P,若∠PBC=70°,则∠MPC的度数为( )| A. | 55° | B. | 40° | C. | 35° | D. | 20° |
 如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长.
如图所示,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AD=3cm,求AB,AC的长.