题目内容
6. 如图所示,在Rt△ACB中,∠ACB=90°,M为AB上一点,且MB=MC,求证:MA=MC.
如图所示,在Rt△ACB中,∠ACB=90°,M为AB上一点,且MB=MC,求证:MA=MC.请在下面证明过程中的括号内填上适当的理由.
证明:∵MB=MC(已知)
∴∠B=∠2(等边对等角).
又∵∠ACB=90°.
∴∠1-∠2=(90°),∠A+(∠B)=90°.
∴∠A=∠1(等量代换),∴MA=MC(等角对等边)
分析 根据等腰三角形的性质得到∠B=∠2,由∠ACB=90°.得到∠1+∠2=90°,∠A+∠B=90°.等量代换得到∠A=∠1,根据等腰三角形的判定即可得到结论.
解答 证明:∵MB=MC(已知)
∴∠B=∠2(等边对等角).
又∵∠ACB=90°.
∴∠1+∠2=(90°),∠A+(∠B)=90°,
∴∠A=∠1(等量代换),
∴MA=MC(等角对等边).
故答案为:等边对等角,90°,∠B,等量代换,等角对等边.
点评 本题考查了等腰三角形的判定和性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
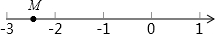 在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( )
在数轴上,点M的位置如图所示,设点M表示有理数m,点P表示m的相反数,点Q表示m的倒数,点N表示m的绝对值,点R表示m的平方.则这些点中,一定与M位于原点同侧的点是( ) 如图,点D是△ABC的边AC上一点,且AB=CD,∠BAC=60°,点E是BD的中点.求证:BC=2AE.
如图,点D是△ABC的边AC上一点,且AB=CD,∠BAC=60°,点E是BD的中点.求证:BC=2AE. 如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH. 如图,平行四边形ABCD∽平行四边形AEFG,若平行四边形ABCD周长为60cm,AF=12cm,FC=8cm,则平行四边形AEFG的周长是36cm.
如图,平行四边形ABCD∽平行四边形AEFG,若平行四边形ABCD周长为60cm,AF=12cm,FC=8cm,则平行四边形AEFG的周长是36cm.