题目内容
13.(1)($\frac{1}{2}$)-1-2cos30°+$\sqrt{27}$+(2-π)0(2)解不等式组$\left\{\begin{array}{l}{3x≥4x-1}\\{\frac{5x-1}{2}>x-2}\end{array}\right.$.
分析 (1)本题涉及负整数指数幂、特殊角的三角函数值、二次根式化简、零指数幂4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)($\frac{1}{2}$)-1-2cos30°+$\sqrt{27}$+(2-π)0
=2-2×$\frac{\sqrt{3}}{2}$+3$\sqrt{3}$+1
=2-$\sqrt{3}$+3$\sqrt{3}$+1
=3+2$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{3x≥4x-1①}\\{\frac{5x-1}{2}>x-2②}\end{array}\right.$,
由①得,x≤1;
由②得,x>-1,
故此不等式组的解集为:-1<x≤1.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、特殊角的三角函数值、二次根式、零指数幂等考点的运算.同时考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
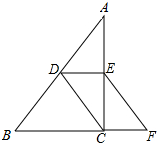 如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.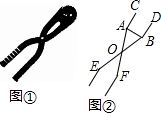 双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)
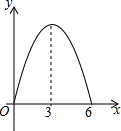
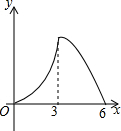
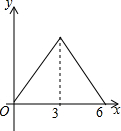
双十一期间,某店铺推出的如图①所示的雪球夹销售火爆,其形状可近似的看成图②所示的图形,当雪球夹闭合时,测得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(精确到1厘米)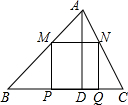 锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )
锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动,且MN∥BC,MP⊥BC,NQ⊥BC得矩形MPQN,设MN的长为X,矩形MPQN的面积为Y,则y关于x的函数图象大致形状是( )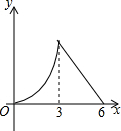
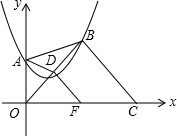 如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.
如图,抛物线y=a(x-1)2+$\sqrt{2}$(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为$\frac{\sqrt{2}}{2}$.