题目内容
1.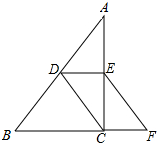 如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,点F是BC延长线上一点,且CF=$\frac{1}{2}$BC,连结CD、EF.求证:CD=EF.
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,DE=$\frac{1}{2}$BC,然后求出四边形DEFC是平行四边形,再根据平行四边形的对边相等证明即可.
解答 证明:∵D、E分别是边AB、AC的中点,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∵CF=$\frac{1}{2}$BC,
∴DE=CF,
∴四边形DEFC是平行四边形,
∴CD=EF.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定与性质,熟记定理并确定出平行四边形是解题的关键.

练习册系列答案
相关题目
9.下列方程中,有两个相等的实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-1=0 |
10.下列判断正确的是( )
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
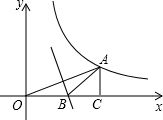 如图,点A在反比例函数y=$\frac{4}{x}$(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为2$\sqrt{6}$.
如图,点A在反比例函数y=$\frac{4}{x}$(x>0)图象上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B.则△ABC的周长为2$\sqrt{6}$.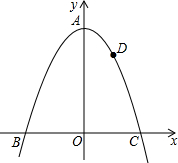 如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.
如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为3$\sqrt{2}$.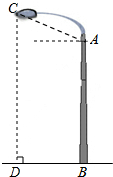 如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)
如图,某广场有一灯柱AB高7.5米,灯的顶端C离灯柱顶端A的距离CA为1.7米,且∠CAB=110°,求灯的顶端C距离地面的高度CD.(结果精确到0.1米)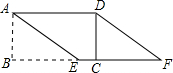 如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.
如图,面积为15的矩形纸片ABCD中,AD=5,在BC边上取点E,使AE=5,剪下△ABE,将它平移至△DCF的位置,拼成四边形AEFD.