题目内容
20.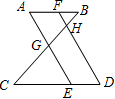 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )
如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )| A. | $\frac{DH}{FH}=\frac{CH}{BH}$ | B. | $\frac{GE}{FD}=\frac{CG}{CB}$ | C. | $\frac{AF}{CE}=\frac{HG}{CG}$ | D. | $\frac{FH}{AG}=\frac{BF}{FA}$ |
分析 根据平行线分线段成比例定理得出比例式,再变形,即可判断各个选项.
解答 解:A、∵AB∥CD,
∴$\frac{DH}{FH}$=$\frac{CH}{BH}$,故本选项不符合题目要求;
B、∵AE∥DF,
∴△CEG∞△CDH,
∴$\frac{GE}{DH}$=$\frac{CG}{CH}$,
∴$\frac{EG}{CG}$=$\frac{DH}{CH}$,
∵AB∥CD,
∴$\frac{CH}{CB}$=$\frac{DH}{DF}$,
∴$\frac{DH}{CH}$=$\frac{DF}{CB}$,
∴$\frac{GE}{CG}$=$\frac{DF}{CB}$,
∴$\frac{GE}{FD}$=$\frac{CG}{CB}$,故本选项不符合题目要求;
∵AB∥CD,AE∥DF,
∴四边形AEDF是平行四边形,
∴AF=DE,
∵AE∥DF,
∴$\frac{DE}{CE}=\frac{HG}{CG}$,
∴$\frac{AF}{CE}$=$\frac{HG}{CG}$,故本选项不符合题目要求;
D、∵AE∥DF,
∴△BFH∞△BAG,
∴$\frac{FH}{AG}=\frac{BF}{BA}$,故本选项符合题目要求;
故选D.
点评 本题考查了平行线分线段成比例定理,相似三角形的性质和判定的应用,能根据定理得出比例式是解此题的关键.

练习册系列答案
相关题目
10.计算(-2)0+1的结果( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.已知二次三项式x2-kx-15能分解成系数为整数的两个一次因式的积,则整数k的取值范围有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.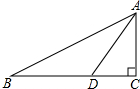 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |

 如图,在半径为4cm的⊙O中,劣弧AB的长为2πcm,则∠C=45度.
如图,在半径为4cm的⊙O中,劣弧AB的长为2πcm,则∠C=45度.