题目内容
5．
如图，在半径为4cm的⊙O中，劣弧AB的长为2πcm，则∠C=45度．
分析 根据弧长公式l=$\frac{nπR}{180}$，可得n=$\frac{180l}{πR}$，求出n的值，即为∠AOB的度数，再根据圆周角定理即可求出∠C．
解答 解：∵l=$\frac{nπR}{180}$，
∴n=$\frac{180l}{πR}$=$\frac{180×2π}{π×4}$=90，
∴∠AOB=90°，
∴∠C=$\frac{1}{2}$∠AOB=45．
故答案为45．
点评 本题考查了弧长公式l=$\frac{nπR}{180}$（弧长为l，圆心角度数为n，圆的半径为R），圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．求出∠AOB的度数是解题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
15．下列图形不是由平移而得到的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
16．移动互联网已全面进入人们的日常生活，截至2016年2月，孝感市4G用户总数达到3820000，数据3820000用科学记数法表示为（ ）
| A． | 3.8×106 | B． | 3.82×105 | C． | 3.82×106 | D． | 3.82×107 |
20．
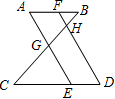如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（ ）
如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（ ）| A． | $\frac{DH}{FH}=\frac{CH}{BH}$ | B． | $\frac{GE}{FD}=\frac{CG}{CB}$ | C． | $\frac{AF}{CE}=\frac{HG}{CG}$ | D． | $\frac{FH}{AG}=\frac{BF}{FA}$ |
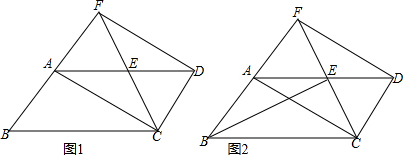
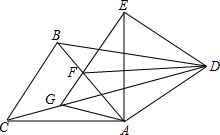如图，两个等边△ABC，△ADE顶点A重合，过点E作BC的平行线，分别交AB，CD于F，G．
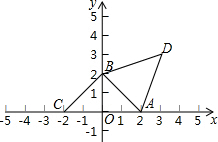如图，在平面直角坐标系xOy中，A，B两点分别在x轴、y轴的正半轴上，OA=OB=2．