题目内容
8.(1)解方程:$\frac{x}{x-2}-1=\frac{1}{{{x^2}-4}}$(2)解方程组:$\left\{{\begin{array}{l}{y=2x-4}\\{3x+y=1}\end{array}}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程组利用代入消元法求出解即可.
解答 解:(1)去分母得:x2+2x-x2+4=1,
解得:x=-1.5,
经检验x=-1.5是分式方程的解;
(2)$\left\{\begin{array}{l}{y=2x-4①}\\{3x+y=1②}\end{array}\right.$,
把①代入②得:3x+2x-4=1,
解得:x=1,
把x=1代入①得:y=-2,
则方程组的解为$\left\{{\begin{array}{l}{x=1}\\{y=-2}\end{array}}\right.$.
点评 此题考查了解分式方程,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
18.下列各数中,最小的是( )
| A. | -$\sqrt{2}$ | B. | 0 | C. | -1 | D. | -$\sqrt{3}$ |
16.移动互联网已全面进入人们的日常生活,截至2016年2月,孝感市4G用户总数达到3820000,数据3820000用科学记数法表示为( )
| A. | 3.8×106 | B. | 3.82×105 | C. | 3.82×106 | D. | 3.82×107 |
3.据报道,2014年第一季度,广东省实现地区生产总值约1.36万亿元,用科学记数法表示为( )
| A. | 0.136×1012元 | B. | 1.36×1012元 | C. | 1.36×1011元 | D. | 13.6×1011元 |
20.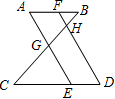 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )
如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )
 如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )
如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是( )| A. | $\frac{DH}{FH}=\frac{CH}{BH}$ | B. | $\frac{GE}{FD}=\frac{CG}{CB}$ | C. | $\frac{AF}{CE}=\frac{HG}{CG}$ | D. | $\frac{FH}{AG}=\frac{BF}{FA}$ |
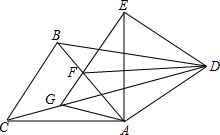 如图,两个等边△ABC,△ADE顶点A重合,过点E作BC的平行线,分别交AB,CD于F,G.
如图,两个等边△ABC,△ADE顶点A重合,过点E作BC的平行线,分别交AB,CD于F,G.