题目内容
9．
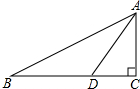如图，在△ABC中，∠C=90°，AC=2，点D在BC上，∠ADC=2∠B，AD=$\sqrt{5}$，则BC的长为（ ）| A． | $\sqrt{3}$-1 | B． | $\sqrt{3}$+1 | C． | $\sqrt{5}$-1 | D． | $\sqrt{5}$+1 |
分析 根据∠ADC=2∠B，∠ADC=∠B+∠BAD判断出DB=DA，根据勾股定理求出DC的长，从而求出BC的长．
解答 解：∵∠ADC=2∠B，∠ADC=∠B+∠BAD，
∴∠B=∠DAB，
∴DB=DA=$\sqrt{5}$，
在Rt△ADC中，
DC=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{5-1}$=1，
∴BC=$\sqrt{5}$+1．
故选D．
点评 本题主要考查了勾股定理，关键是熟练掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．同时涉及三角形外角的性质，二者结合，是一道好题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
20．
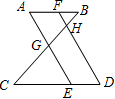如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（ ）
如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（ ）| A． | $\frac{DH}{FH}=\frac{CH}{BH}$ | B． | $\frac{GE}{FD}=\frac{CG}{CB}$ | C． | $\frac{AF}{CE}=\frac{HG}{CG}$ | D． | $\frac{FH}{AG}=\frac{BF}{FA}$ |
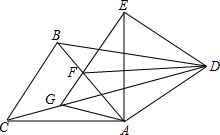如图，两个等边△ABC，△ADE顶点A重合，过点E作BC的平行线，分别交AB，CD于F，G．
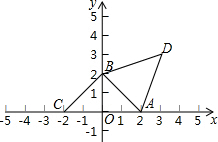如图，在平面直角坐标系xOy中，A，B两点分别在x轴、y轴的正半轴上，OA=OB=2．
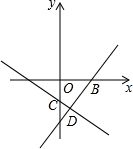已知：如图，一次函数y=$\frac{4}{3}$x+n与x轴交于点B，一次函数y=-$\frac{2}{3}$x+m与y轴交于点C，且它们的图象都经过点D（1，-$\frac{8}{3}$）．