题目内容
13.已知y是x的一次函数,且当x=-4时,y=9;当x=6时,y=-1.(1)求这个一次函数的解析式;
(2)当x=-$\frac{1}{2}$时,求函数y的值;
(3)求当-3<y≤1时,自变量x取值范围.
分析 (1)首先设出这个一次函数的解析式为y=kx+b(k≠0),再利用待定系数法可得方程组$\left\{\begin{array}{l}{-4k+b=9}\\{6k+b=-1}\end{array}\right.$,再解方程组可得k、b的值,进而得到解析式y=-x+5;
(2)把x=-$\frac{1}{2}$代入y=-x+5中计算出y的值即可;
(3)根据k的值可得y随x的增大而减小,然后计算出y=-3时x的值,y=1时x的值,进而得到x的取值范围.
解答 解:(1)设这个一次函数的解析式为y=kx+b(k≠0),
∵当x=-4时,y=9;当x=6时,y=-1,
∴$\left\{\begin{array}{l}{-4k+b=9}\\{6k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
故这个一次函数的解析式为y=-x+5;
(2)把x=-$\frac{1}{2}$代入y=-x+5中得:
y=$\frac{1}{2}$+5=5$\frac{1}{2}$;
(3)∵k=-1,
∴y随x的增大而减小,
当y=-3时,-3=-x+5,x=8,
当y=1时,1=-x+5,x=4,
故当-3<y≤1时,自变量x取值范围,4≤x<8.
点评 此题主要考查了待定系数法求一次函数解析式,以及求函数解析式的值,一次函数的性质,关键是计算出一次函数的解析式.

练习册系列答案
相关题目
3.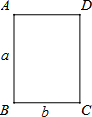 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD中,AB=a,BC=b,a>b,以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙,记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙,S甲=S乙 | B. | V甲<V乙,S甲=S乙 | C. | V甲=V乙,S甲=S乙 | D. | V甲>V乙,S甲<S乙 |
4.有一个三位数,现将它最左边的数字移至最右边所得到的数比原来的数小144;而由它的十位数字与个位数字所组成的两位数除以百位数字,商是7,余数是4.如果设这个三位数的百位为x,十位与个位数字组成的两位数为y,可得方程组是( )
| A. | $\left\{\begin{array}{l}{(100x+y)-(100y+x)=144}\\{y=7x+4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{(100x+y)-(10y+x)=144}\\{y=7x+4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{(10y+x)-(100x+y)=144}\\{y=7x+4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{(100x+y)-(10x+y)=144}\\{y=7x+4}\end{array}\right.$ |
1.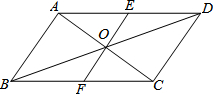 如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
 如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )
如图,平行四边形ABCD中,EF过对角线的交点O,AB=3,AD=4,OF=1.3,则四边形ABEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
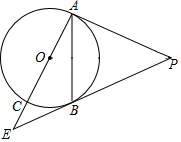 如图,PA,PB是⊙O的切线,切点分别为A,B,AC是⊙O的直径,AC,PB的延长线交于点E,若tan∠BAE=$\frac{1}{2}$,求sin∠E的值.
如图,PA,PB是⊙O的切线,切点分别为A,B,AC是⊙O的直径,AC,PB的延长线交于点E,若tan∠BAE=$\frac{1}{2}$,求sin∠E的值. 解不等式15-9x<10-4x,并把解集在数轴上表示出来.
解不等式15-9x<10-4x,并把解集在数轴上表示出来. 如图,已知AB∥DE,D是BC的中点,∠A=∠E,证明:△ABD≌△EDC.
如图,已知AB∥DE,D是BC的中点,∠A=∠E,证明:△ABD≌△EDC.