Question

1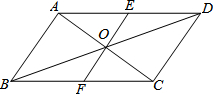．如图，平行四边形ABCD中，EF过对角线的交点O，AB=3，AD=4，OF=1.3，则四边形ABEF的周长为（　　）

• A． 8.3
• B． 9.6
• C． 12.6
• D． 13.6

Answer 1

分析 只要证明△EDO≌△FBO，可得DE=BF，OE=OF=1.3，所以四边形ABFE的周长=AB+BF+EF+AE=AB+（DE+AE）+EF=AB+AD+EF，由此即可解决问题．

解答 解：∵四边形ABCD是平行四边形，
∴AD=BC=4，AD∥BC，OD=OB，
∠EDO=∠FBD，
在△EDO和△FBO中，
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OD=OB}\\{∠EOD=∠BOF}\end{array}\right.$，
∴△EDO≌△FBO，
∴DE=BF，OE=OF=1.3，
∴四边形ABFE的周长=AB+BF+EF+AE=AB+（DE+AE）+EF=AB+AD+EF=3+4+2.6=9.6，
故选B．

点评 本题考查平行四边形的性质、全等三角形的判定和性质、四边形周长的定义等知识，解题的关键是熟练应用全等三角形解决问题，属于中考常考题型．