题目内容
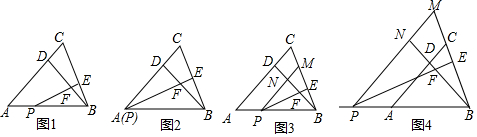
14.问题情境:数学活动课上,同学们探究等腰三角形中两条线段的关系:如图1,△ABC中,AB=AC,∠BAC=45°,点D是边AC上的一点,且DA=DB,点P是边AB上一点(不与点B重合),过点P作PE⊥BC,垂足为点E,交线段BD于点F.线段PF与BE之间存在怎样的数量关系?
特例猜想:
(1)为探究问题的一般结论,同学们先研究特殊情况:当点P与点A重合时,如图2,小彬猜想得到①△ADF≌△BDC;②PF=2BE.请你判断这两个猜想是否正确,并说明理由;
一般探究:
(2)通过特例启发,同学们广开思路,进行了如下探究.
请从下列A,B两题中任选一题作答:我选择A或B题:
A:如图3,勤学小组发现图1中PF=2BE也成立.他们的思路是:在图1中的BD上取一点N,使得PN=NB,延长PN交BC于点M,得到图3,证明了△PNF≌△BNM,….请你根据勤学小组的思路接着完成说明PF=2BE的过程.
B:善思小组探究了更加一般的情况,当图1中的点P运动到线段BA的延长线上,如图4,其余条件不变,发现此时PF=2BE也成立.他们的思路是:在BD的延长线上取一点N,使得PN=NB,延长PN交BC的延长线于点M,….请你根据善思小组的思路说明图4中的PF=2BE.
分析 (1)这两个结论都是正确的.根据AAS或ASA即可证明△ADF≌△BDC,推出PF=BC,再证明BC=2BE即可解决问题;
(2)A、B的证明思路差不多.只要证明△PNF≌△BNM,即可解决问题;
解答 解:(1)这两个结论都是正确的,理由如下: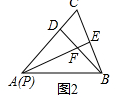 如图2中,
如图2中,
∵DA=DB,
∴∠DBA=∠BAC,
∵∠BAC=45°,
∴∠DBA=45°,
∴∠ADB=180°∠DAB-∠ABD=180°-45°-45°=90°,
∴∠BDC=180°-∠ADB=90°,
∴∠ADB=∠BDC,
∵PE⊥BC,
∴∠PEC=90°,
∴∠C+∠DAF=90°,∠DAF+∠AFD=90°,
∴∠C=∠AFD,
在△ADF和△BDC中,
$\left\{\begin{array}{l}{∠AFD=∠C}\\{∠ADF=∠BDC}\\{AD=BD}\end{array}\right.$,
∴△ADF≌△BDC.故①正确,
∴AF=BC,即PF=BC,
∵AB=AC,PE⊥BC,
∴BC=2BE,
∴PF=2BE.故②正确.
(2)A:如图3中,由(1)可知,△PNF≌△BNM,
∴PF=BM,
∵NP=NB,
∴∠NPB=∠NBP,
∵∠ABD=45°,
∴∠BAC=∠NPB=45°,
∴PM∥AC,
∴∠PMB=∠C,
∵AB=AC,
∴∠C=∠ABC,
∴∠PMB=∠ABC,
∴PB=PM,∵PE⊥BC,
∴EM=BE,即BM=2BE,
∴PF=2BE
B:如图4中∵NP=NB,
∴∠NPB=∠NBP=∠ABD,
由(1)可知,∠ABD=∠DAB=45°,
∴∠NPB=∠DAB=45°,
∴PM∥AC,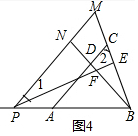
∴∠PNB=∠ADB=90°,
∵∠PNB+∠BNM=90°,∴∠BNM=90°,
∴∠1+∠PFN=90°,
∵PE⊥BM,
∴∠PEM=∠PEB=90°,∠1+∠M=90°,
∴∠M=∠PFN,
∵∠BNM=∠PNF,PN=BN,
∴△PNF≌△BNM,
∴PF=BM,
∵PM∥AC,
∴∠M=∠2,
∵AB=AC,
∴∠2=∠ABC,
∴∠M=∠ABC,
∴PM=PB,∵PE⊥BM,
∴EM=BE,即BM=2BE,
∴PF=2BE.
故答案为A或B.
点评 本题考查三角形综合题、等腰三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )| A. | 2米 | B. | 2.5米 | C. | 2.4米 | D. | 2.1米 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
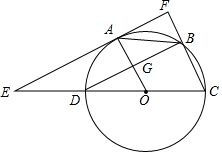 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.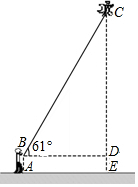 小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m).
小蓝周末去广场放风筝,如图,当风筝飞到点C处时的线长BC约为25m,此时小蓝正好站在点A处,并测得∠CBD=61°,牵引底端B距离地面1.5m,则此时风筝距离地面的高度CE约为23.3m(用科学计算器计算,结果精确到0.1m).