题目内容
4.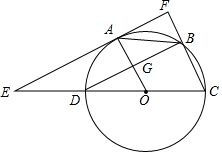 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.(1)求证:EF是⊙O的切线;
(2)求AE的长.
分析 (1)利用圆周角定理得到∠DBC=90°,再利用平行四边形的性质得AO∥BC,所以BD⊥OA,加上EF∥BD,所以OA⊥EF,于是根据切线的判定定理可得到EF是⊙O的切线;
(2)连接OB,如图,利用平行四边形的性质得OA=BC,则OB=OC=BC,于是可判断△OBC为等边三角形,所以∠C=60°,易得∠AOE=∠C=60°,然后在Rt△OAE中利用正切的定义可求出AE的长.
解答 (1)证明:∵CD为直径,
∴∠DBC=90°,
∴BD⊥BC,
∵四边形OABC是平行四边形,
∴AO∥BC,
∴BD⊥OA,
∵EF∥BD,
∴OA⊥EF,
∴EF是⊙O的切线;
(2)解:连接OB,如图,
∵四边形OABC是平行四边形,
∴OA=BC,
而OB=OC=OA,
∴OB=OC=BC,
∴△OBC为等边三角形,
∴∠C=60°,
∴∠AOE=∠C=60°,
在Rt△OAE中,∵tan∠AOE=$\frac{AE}{OA}$,
∴AE=3tan60°=3$\sqrt{3}$.
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;也考查了平行四边形的性质和解直角三角形.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
14.下列关于正方形的叙述,正确的是( )
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
12.对一组数据:-2,1,2,1,下列说法不正确的是( )
| A. | 平均数是1 | B. | 众数是1 | C. | 中位数是1 | D. | 极差是4 |
16.估计$\sqrt{32}$-$\sqrt{16}$÷2的运算结果在哪两个整数之间( )
| A. | 0和1 | B. | 1和2 | C. | 2和3 | D. | 3和4 |
 如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.
如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG. 已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).
已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).