题目内容
8. 如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.
如图在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°.求∠BEC的度数.
分析 先根据AD⊥BC得出∠FDB=90°,根据直角三角形的性质得出∠FBD的度数,再由三角形内角和定理得出∠C的度数,在△BEC中,根据∠BEC=180°-∠FBD-∠C即可得出结论.
解答 解:∵AD⊥BC,
∴∠FDB=90°.
∵∠BFD=60°,
∴∠FBD=90°-60°=30°.
在△ABC中,
∵∠ABC=45°,∠BAC=75°,
∴∠C=180°-∠ABC-∠BAC=180°-45°-75°=60°.
在△BEC中,∵∠FBD=30°,∠C=60°,
∴∠BEC=180°-∠FBD-∠C=180°-30°-60°=90°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
19. 如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
 如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
如图,已知AB∥CD,∠2=2∠1,则∠3等于( )| A. | 60° | B. | 50° | C. | 80° | D. | 40° |
3.已知关于x的方程2x+4=m-x的解为非负数,则m的取值范围是( )
| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |
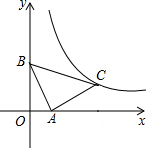 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=$\frac{k}{x}$(x>0)在第一象限内的图象上,则k的值为( )