题目内容
11.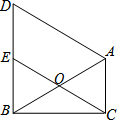 如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.
如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.(1)求证:四边形ACED是平行四边形.
(2)若BC=3,求△ABD的周长.
分析 (1)连接AE,周长四边形ACBE是平行四边形,得出AC∥BE,由AD∥CE,即可得出四边形ACED是平行四边形.
(2)证出四边形ACED是矩形,得出AB=CE=AD,证明△ABD是等边三角形,得出AB=AD=BD,设AC=x,则AB=2AC=2x,在Rt△ABC中,由勾股定理得出方程,解方程求出AB,即可得出答案.
解答 (1)证明:连接AE,如图所示: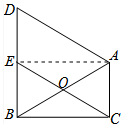
∵O为AB的中点,
∴OA=OB,
∵OC=OE,
∴四边形ACBE是平行四边形,
∴AC∥BE,
∵AD∥CE,
∴四边形ACED是平行四边形.
(2)解:∵∠ACB=90°,四边形ACED是平行四边形.
∴四边形ACED是矩形,
∴AB=CE=AD,
∵∠ABC=30°,
∴∠ABD=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
设AC=x,则AB=2AC=2x,
在Rt△ABC中,由勾股定理得:x2+32=(2x)2,
解得:x=$\sqrt{3}$,
∴AB=2$\sqrt{3}$.
∴△ABD的周长=3AB=6$\sqrt{3}$.
点评 本题考查了平行四边形的判定与性质、矩形的判定与性质、勾股定理、直角三角形的性质、等边三角形的判定与性质;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.m16可以写成( )
| A. | m8+m8 | B. | m8•m8 | C. | m2•m8 | D. | m4•m4 |
2.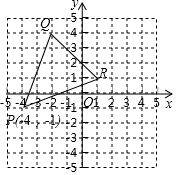 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
 如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )| A. | (-1,-3) | B. | (-2,4) | C. | (-2,-4) | D. | (2,-3) |
19. 如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
 如图,已知AB∥CD,∠2=2∠1,则∠3等于( )
如图,已知AB∥CD,∠2=2∠1,则∠3等于( )| A. | 60° | B. | 50° | C. | 80° | D. | 40° |
3.已知关于x的方程2x+4=m-x的解为非负数,则m的取值范围是( )
| A. | m>$\frac{4}{3}$ | B. | m≥4 | C. | m<4 | D. | m≤$\frac{4}{3}$ |