题目内容
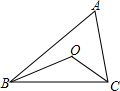 如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )
如图,在△ABC中,∠A=55°,AB、AC的垂直平分线交于点O,则∠BOC的度数为( )| A、35° | B、60° |
| C、110° | D、150° |
考点:线段垂直平分线的性质
专题:
分析:连接OA,根据线段垂直平分线求出OA=OB,OA=OC,推出∠OAB=∠OBA,∠OAC=∠OCA,求出∠OBA+∠OCA=55°,∠ABC+∠CB=125°,求出∠OBC+∠OCB=70°,根据三角形内角和定理求出即可.
解答: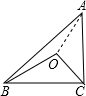
解:连接OA,
∵AB、AC的垂直平分线交于点O,
∴AO=BO,AO=CO,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BAC=55°,
∴∠OBA+∠OCA=55°,∠ABC+∠CB=180°-55°=125°,
∴∠OBC+∠OCB=125°-55°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=110°,
故选C.

解:连接OA,
∵AB、AC的垂直平分线交于点O,
∴AO=BO,AO=CO,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∵∠BAC=55°,
∴∠OBA+∠OCA=55°,∠ABC+∠CB=180°-55°=125°,
∴∠OBC+∠OCB=125°-55°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=110°,
故选C.
点评:本题考查了等腰三角形性质,三角形的内角和定理,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
因式分解x2-16的结果是( )
| A、(x+4)(x-4) |
| B、(x-10)(x-6) |
| C、(x+16)(x-16) |
| D、(x-4)2 |
计算:a4•a4=( )
| A、a0 |
| B、a8 |
| C、a16 |
| D、2a4 |
在①a4•a2②(-a2)3③a12÷a2④a2•a3⑤a3+a3中,计算结果为a6的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知ab=1,M=
,N=
+
,则M与N的关系为( )
| 1 |
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| A、M>N | B、M=N |
| C、M<N | D、不能确定. |
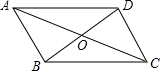 如图,在?ABCD中,已知对角线AC、BD相交于点O.
如图,在?ABCD中,已知对角线AC、BD相交于点O.
 如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由:
如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由: