题目内容
已知a=2+
,b=2-
.
(1)求a2b+ab2的值;
(2)求
-
的值.
| 3 |
| 3 |
(1)求a2b+ab2的值;
(2)求
| a |
| b |
| b |
| a |
考点:二次根式的化简求值
专题:计算题
分析:计算出a+b=4,ab=4-3=1,a-b=2
,
(1)先把原式分解,然后利用整体代入的方法计算;
(2)先通分,再把分子分解得到原式=
,然后利用整体代入的方法计算.
| 3 |
(1)先把原式分解,然后利用整体代入的方法计算;
(2)先通分,再把分子分解得到原式=
| (a+b)(a-b) |
| ab |
解答:解:(1)∵a=2+
,b=2-
.
∴a+b=4,ab=4-3=1,a-b=2
,
(1)原式=ab(a+b)=4×1=4;
(2)原式=
=
=
=8
.
| 3 |
| 3 |
∴a+b=4,ab=4-3=1,a-b=2
| 3 |
(1)原式=ab(a+b)=4×1=4;
(2)原式=
| a2-b2 |
| ab |
=
| (a+b)(a-b) |
| ab |
=
4×2
| ||
| 1 |
=8
| 3 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
计算:a4•a4=( )
| A、a0 |
| B、a8 |
| C、a16 |
| D、2a4 |
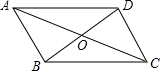 如图,在?ABCD中,已知对角线AC、BD相交于点O.
如图,在?ABCD中,已知对角线AC、BD相交于点O.
 如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由:
如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由: