题目内容
17.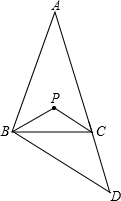 如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )
如图,△ABC中,AB=AC,∠A=40°,延长AC到D,使CD=BC,点P是△ABD的内心,则∠BPC=( )| A. | 105° | B. | 110° | C. | 130° | D. | 145° |
分析 连接PD,如图,连接AP并延长交BC于E,先利用等腰三角形的性质和三角形内角和计算出∠ABC=∠ACB=70°,再利用等腰三角形性质和三角形外角性质可计算出∠CBD=$\frac{1}{2}$∠ACB=35°,则∠ABD=105°,利用三角形内心的性质得AP平分∠BAC,BP平分∠ABD,根据等腰三角形性质可判定AE垂直平分BC,利用角平分线的定义计算出∠PBD=$\frac{1}{2}$∠ABD=52.5°,则∠PBC=22.5°,然后利用PB=PC得到∠PBC=∠PCB=22.5°,最后根据三角形内角和计算∠BPC的度数.
解答 解:连接PD,如图,连接AP并延长交BC于E,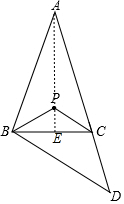
∵AB=AC,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-40°)=70°,
∵CD=CB,
∴∠D=∠CBD,
而∠ACB=∠D+∠CBD,
∴∠CBD=$\frac{1}{2}$∠ACB=35°,
∴∠ABD=35°+70°=105°,
∵点P是△ABD的内心,
∴AP平分∠BAC,BP平分∠ABD,
∴AE垂直平分BC,∠PBD=$\frac{1}{2}$∠ABD=52.5°,
∴∠PBC=52.5°-35°=22.5°,
∵PE垂直平分BC,
∴PB=PC,
∴∠PBC=∠PCB=22.5°,
∴∠BPC=180°-22.5°-22.5°=145°.
故选D.
点评 本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了等腰三角形的性质.

练习册系列答案
相关题目
2.将不等式x-1>0的解集表示在数轴上,下列表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
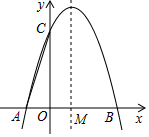 如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.
如图,抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C点,抛物线的对称轴l与x轴交于M点.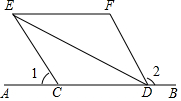 已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
 如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.
如图,在菱形ABCD中,CE垂直对角线AC于点C,AB的延长线交CE于点E.