题目内容
12.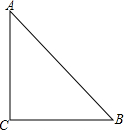 如图,已知在Rt△ABC中,∠C=90°,AC=BC=1,点D在边BC上,将△ABC沿直线AD翻折,使点C落在点C′处,联结AC′,直线AC′与边CB的延长线相交于点F.如果∠DAB=∠BAF,那么BF=$\sqrt{3}$-1.
如图,已知在Rt△ABC中,∠C=90°,AC=BC=1,点D在边BC上,将△ABC沿直线AD翻折,使点C落在点C′处,联结AC′,直线AC′与边CB的延长线相交于点F.如果∠DAB=∠BAF,那么BF=$\sqrt{3}$-1.
分析 在Rt△ABC中,∠C=90°,AC=BC=1,得到∠CAB=∠ABC=45°,由△ADC′是将△ABC沿直线AD翻折得到的,求出∠CAD=∠C′AD,于是得到∠ABF=135°,求得∠F=30°,根据直角三角形的性质即可得到结果.
解答  解:∵在Rt△ABC中,∠C=90°,AC=BC=1,
解:∵在Rt△ABC中,∠C=90°,AC=BC=1,
∴∠CAB=∠ABC=45°,
∵△ADC′是将△ABC沿直线AD翻折得到的,
∴∠CAD=∠C′AD,
∵∠DAB=∠BAF,
∴∠BAD=$\frac{1}{2}$∠DAC=$\frac{1}{3}$∠BAC=15°,
∵∠ABF=135°,
∴∠F=30°,
∴CF=$\frac{AC}{tan30°}$=$\sqrt{3}$,
∴BF=CF-BC=$\sqrt{3}$-1,
故答案为:$\sqrt{3}$-1.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的性质,锐角三角函数,正确的作出图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
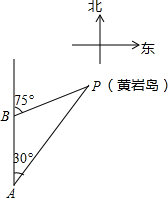 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)
如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1) 某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.
某体育用品公司以每件60元的批发价购回一批“电子智能跳绳”,第一周以每件120元的价格进行销售,第二周以每件110元的价格进行销售,结果两周共销售该款跳绳100件,两周共实现销售额11400元.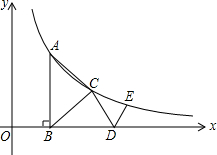 如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.
如图,△ABC是等腰直角三角形,斜边AB⊥x轴于B,顶点A,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,再作等腰Rt△CDE,使直角顶点E在该函数图象上,顶点D在x轴正半轴上,则△CDE的面积是$\frac{11-6\sqrt{3}}{2}$.