题目内容
19．2x+3＜4（x-1）+3≤3x+2．分析 首先解出不等式组的各个不等式x的取值范围，然后求出x的公共部分，该公共部分就是不等式的解．
解答 解：不等式可化为$\left\{\begin{array}{l}2x+3＜4（x-1）+3\;…（1）\\ 4（x-1）+3\;≤3x+2…（2）\end{array}\right.$，
由（1）解得：x＞2，（2分）
由（2）解得：x≤-3．（4分）
∴原不等式组的解集是2＜x≤-3．
点评 本题主要考查解一元一次不等式组，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
7．已知△ABC中，∠A=∠B+∠C，则△ABC的形状是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 等腰三角形 | D． | 钝角三角形 |
某经销商批发了一批无锡水蜜桃，为了打开销路，对1200个水蜜桃进行打包优惠出售，打包方式及售价如图，假设用这两种打包方式恰好装完全部水蜜桃．
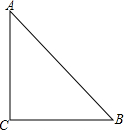如图，已知在Rt△ABC中，∠C=90°，AC=BC=1，点D在边BC上，将△ABC沿直线AD翻折，使点C落在点C′处，联结AC′，直线AC′与边CB的延长线相交于点F．如果∠DAB=∠BAF，那么BF=$\sqrt{3}$-1．