题目内容
12.请从以下两个小题中任选一个作答,若多选,则按第一题计分.A.一个正多边形的每一个外角都是72°,那么这个正多边形是五边形;
B.用科学计算器计算:3-2sin38°19′≈1.76.(结果精确到0.01)
分析 A:根据正多边形的外角和为360°,即可解决问题;
B:利用计算器求出sin38°19′≈0.6193,代入计算即可;
解答 解:A:设边数为n,由题意n=$\frac{360°}{72°}$=5,
所以这个正多边形是五边形,
故答案为五.
B:原式=3-2×0.6193≈1.76.
故答案为1.76.
点评 本题考查正多边形的性质、计算器的应用等知识,解题的关键是记住正多边形的外角和为360°.

练习册系列答案
相关题目
7. 如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )
如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )
 如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )
如图,矩形ABCD中,EG∥AD,EG⊥HF于I,AB=6cm,AD=10cm,矩形AEIH的面积为2cm2,四边形EBFI的面积为4cm2,则△BIC的面积为( )| A. | 40cm2 | B. | 20cm2 | C. | 10cm2 | D. | 6cm2 |
17. 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
 如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )
如图,矩形ABCD中,E、H、F、G为AD、AB、BC、CD边上的点,连结OC、CH,CH交EF于I,EF∥AB,GH∥AD,EF、GH交于O点,如果AE:ED=2:3,AH:HB=1:4,S△OCI=1,则S矩形ABCD的值为( )| A. | $\frac{125}{12}$ | B. | $\frac{125}{24}$ | C. | 40 | D. | 20 |
4. 在图中,梯形的个数为( )
在图中,梯形的个数为( )
 在图中,梯形的个数为( )
在图中,梯形的个数为( )| A. | 6 | B. | 9 | C. | 15 | D. | 27 |
1.用配方法解方程x2-6x=-1得到的方程为( )
| A. | (x-3)2=8 | B. | (x-3)2=-10 | C. | (x+3)2=8 | D. | (x+3)2=-10 |
2.下列事件中,属于随机事件的是( )
| A. | ($\sqrt{a}$)2=a | B. | 若a>b(ab≠0),则$\frac{1}{a}$<$\frac{1}{b}$ | ||
| C. | |a|•|b|=|ab| | D. | 若m为整数,则(m+$\frac{1}{2}$)2+$\frac{7}{4}$是整数 |
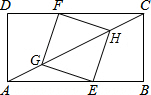 如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.
如图,矩形ABCD中,AB=4,BC=2,四边形EGFH是正方形,当点E在AB上,点F在CD上,点A,C,G,H在同一条直线上时,CH的长是$\frac{\sqrt{5}}{2}$.