题目内容
15.解方程:(1)4(2x-1)2=9(x-3)2;
(2)2y2-5y-3=0.
分析 (1)先把等号右边的式子移到等号的左边,再根据平方差公式进行因式分解,然后即可得出答案;
(2)根据式子相乘法把给出的式子进行因式分解,然后求解即可.
解答 解:(1)4(2x-1)2=9(x-3)2,
4(2x-1)2-9(x-3)2=0,
[2(2x-1)+3(x-3)][2(2x-1)-3(x-3)]=0,
(7x-11)(x+7)=0,
x1=$\frac{11}{7}$,x2=-7;
(2)2y2-5y-3=0,
(2y+1)(y-3)=0,
y1=-$\frac{1}{2}$,y=3.
点评 此题考查了因式分解法解一元二次方程,因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;
③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.

练习册系列答案
相关题目
11.无理数a满足:2<a<3,那么a可能是( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{11}$ | D. | $\sqrt{10}$ |

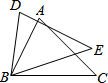 如图,AB=DB,∠ABD=∠CBE,请添加一个适当的条件:BC=BE(只需添加一个即可),使△ABC≌△DBE.理由是SAS.
如图,AB=DB,∠ABD=∠CBE,请添加一个适当的条件:BC=BE(只需添加一个即可),使△ABC≌△DBE.理由是SAS.