题目内容
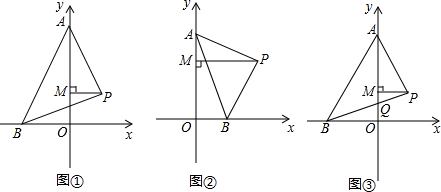
4.平面直角坐标系中,P(2,2),以P为直角顶点作∠APB=90°,过P作PM⊥y轴.(1)如图①,试判新AM、OB、PM的关系;
(2)如图②,试判断AM、OB、PM的关系;
(3)如阳③,若y轴恰好平分∠PAB,PB与y轴交于Q点.求证:$\frac{PM+MQ}{BO}$为定值.
分析 (1)过P作PH⊥x轴,交于H,则四边形OHPM为矩形,得出OH=PM,∠HPM=∠APB=90°,由ASA证明△BHP≌△AMP,得出AM=BH=OB+OH=OB+PM即可;
(2)过P作PH⊥x轴,交于H,则四边形OHPM为矩形,得出OH=PM,∠HPM=∠APB=90°,由ASA证明△BHP≌△AMP,得出AM=BH,即可得出结论;
(3)延长AP交x轴于F,过P作PH⊥x轴,交于H,证出BO=OF,∠FPH=∠QPM,由ASA证明△PMQ≌△PHF,得出MQ=HF,即可得出结论.
解答 (1)解:过P作PH⊥x轴,交于H,如图1所示: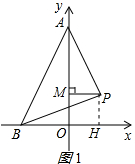
∵PM⊥y轴,
∴四边形OHPM为矩形,
∴OH=PM,∠HPM=∠APB=90°,
∴∠BPH=∠MPA,
∵P(2,2),
∴MP=PH=2,
在△BHP和△AMP中,
$\left\{\begin{array}{l}{∠BPH=∠MPA}\\{PH=MP}\\{∠BHP=∠AMP=90°}\end{array}\right.$,
∴△BHP≌△AMP(ASA),
∴AM=BH=OB+OH=OB+PM;
(2)解:过P作PH⊥x轴,交于H,如图2所示: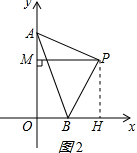 ∵PM⊥y轴,
∵PM⊥y轴,
∴四边形OHPM为矩形,
∴OH=PM,∠HPM=∠APB=90°,
∴∠BPH=∠MPA,
∵P(2,2),
∴MP=PH=2,
在△BHP和△AMP中,
$\left\{\begin{array}{l}{∠BPH=∠MPA}\\{PH=MP}\\{∠BHP=∠AMP=90°}\end{array}\right.$,
∴△BHP≌△AMP(ASA),
∴AM=BH,
∴PM=OB+BH=OB+AM;
(3)证明:延长AP交x轴于F,过P作PH⊥x轴,交于H,如图3所示: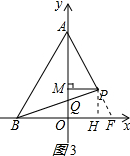
∵y轴平分∠PAB,AO⊥BF,
∴BO=OF,
∵P(2,2),
∴MP=PH=2,
∵∠FPB=∠APB=90°,
∴∠FPH=∠QPM,
在△PMQ和△PHF中,
$\left\{\begin{array}{l}{∠FPH=∠QPM}\\{PH=PM}\\{∠PHF=∠PMQ=90°}\end{array}\right.$,
∴△PMQ≌△PHF(ASA),
∴MQ=HF,
∴$\frac{PM+MQ}{OB}$=$\frac{OH+HF}{OB}$=$\frac{OF}{OB}$=1,
∴$\frac{PM+MQ}{BO}$为定值.
点评 本题考查了全等三角形的判定与性质、矩形的判定与性质、坐标与图形性质等知识;本题综合性强,难度较大,需要通过作辅助线证明三角形全等才能得出结论.

 如图,四边形ABCD外接圆O,若∠BOD=138°,则他的外角∠DCE等于多少( )
如图,四边形ABCD外接圆O,若∠BOD=138°,则他的外角∠DCE等于多少( )| A. | 69° | B. | 42° | C. | 48° | D. | 38° |
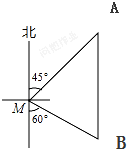 如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.求渔船从A到B的航行距离.
如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.求渔船从A到B的航行距离. 已知线段CD,延长CD到B,使DB=2CD,反向延长CD到A,使CA=CB,若CD=2cm,求AB的长.
已知线段CD,延长CD到B,使DB=2CD,反向延长CD到A,使CA=CB,若CD=2cm,求AB的长. 已知点O是平行四边形ABCD对角线的交点,则图中关于点O对称的三角形有4对.
已知点O是平行四边形ABCD对角线的交点,则图中关于点O对称的三角形有4对.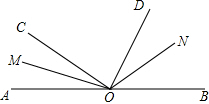 如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求:
如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线.求: