题目内容
15.已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:AH=AB;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
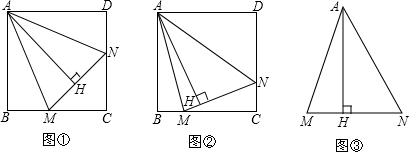
分析 (1)由三角形全等可以证明AH=AB,
(2)延长CB至E,使BE=DN,证明△AEM≌△ANM,能得到AH=AB,
(3)分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,然后分别延长BM和DN交于点C,得正方形ABCE,设AH=x,则MC=x-2,NC=x-3,在Rt△MCN中,由勾股定理,解得x.
解答 解:(1)如图①AH=AB,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在△ABM与△ADN中,$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠D}\\{BM=DN}\end{array}\right.$,
∴△ABM≌△ADN,
∴∠BAM=∠DAN,AM=AN,
∵AH⊥MN,
∴∠MAH=$\frac{1}{2}$MAN=22.5°,
∵∠BAM+∠DAN=45°,
∴∠BAM=22.5°,
在△ABM与△AHM中,$\left\{\begin{array}{l}{∠BAM=∠HAM}\\{∠B=∠AHM=90°}\\{AM=AM}\end{array}\right.$,
∴△ABM≌△AHM,
∴AB=AH;
故答案为:AH=AB;
(2)数量关系成立.如图②,延长CB至E,使BE=DN.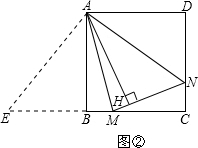 ∵ABCD是正方形,
∵ABCD是正方形,
∴AB=AD,∠D=∠ABE=90°,
在Rt△AEB和Rt△AND中,$\left\{\begin{array}{l}{AB=AD}\\{∠ABE=∠ADN}\\{BE=DN}\end{array}\right.$,
∴Rt△AEB≌Rt△AND,
∴AE=AN,∠EAB=∠NAD,
∴∠EAM=∠NAM=45°,
在△AEM和△ANM中,$\left\{\begin{array}{l}{AE=AN}\\{∠EAM=∠NAM}\\{AM=AM}\end{array}\right.$,
∴△AEM≌△ANM,
∴S△AEM=S△ANM,EM=MN,
∵AB、AH是△AEM和△ANM对应边上的高,
∴AB=AH;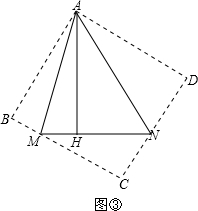 (3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,
(3)如图③分别沿AM、AN翻折△AMH和△ANH,得到△ABM和△AND,
∴BM=2,DN=3,∠B=∠D=∠BAD=90°,
分别延长BM和DN交于点C,得正方形ABCD,
由(2)可知,AH=AB=BC=CD=AD,
设AH=x,则MC=x-2,NC=x-3,
在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,
∴52=(x-2)2+(x-3)2,
解得x1=6,x2=-1(不符合题意,舍去)
∴AH=6.
点评 本题考查了正方形的性质,全等三角形的性质和判定,勾股定理,翻折的性质,此题比较典型,具有一定的代表性,且证明过程类似,同时通过做此题培养了学生的猜想能力和类比推理能力.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
| A. | a3+a3=a6 | B. | a2•a3=a5 | C. | (ab2)3=a3b3 | D. | a10÷a2=a5 |
 如图,由四个小正方体叠成一个立体图形,其俯视图是( )
如图,由四个小正方体叠成一个立体图形,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
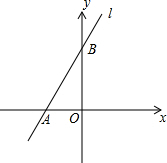 如图,直线l与x轴相交于点A(-2,0),与y轴相交于点B,∠BAO=60°.
如图,直线l与x轴相交于点A(-2,0),与y轴相交于点B,∠BAO=60°.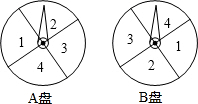 小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).
小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).