题目内容
5.先化简:$\frac{1}{x+1}$÷($\frac{{x}^{2}-2x+1}{{x}^{2}-1}$+$\frac{1}{x}$),再从-2≤x≤2的范围内选取一个你认为合理的x的整数值带入求原式的值.分析 将括号内分式分子、分母因式分解后约分,再通分计算括号内分式的加法,最后将除法转化为乘法约分后即可化简,再在-2≤x≤2的范围内选取一个合理的x的整数值代入原式求值.
解答 解:原式=$\frac{1}{x+1}$÷[$\frac{(x-1)^{2}}{(x+1)(x-1)}$+$\frac{1}{x}$]
=$\frac{1}{x+1}$÷($\frac{x-1}{x+1}$+$\frac{1}{x}$)
=$\frac{1}{x+1}$÷$\frac{{x}^{2}-x+x+1}{x(x+1)}$
=$\frac{1}{x+1}$×$\frac{x(x+1)}{{x}^{2}+1}$
=$\frac{x}{{x}^{2}+1}$,
当x=2时,原式=$\frac{2}{{2}^{2}+1}$=$\frac{2}{5}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的性质及运算步骤是解题的关键,取x的整数值时要注意确保分式有意义.

练习册系列答案
相关题目
20.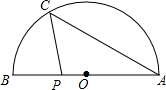 如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
 如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )
如图,AB是半圆O的直径,点C在半圆周上,连结AC,∠BAC=30°,点P是线段AB上任意一点,若AB=4,则CP的长不可能为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
10. 如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
 如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
17.下列计算正确的是( )
| A. | 5$\sqrt{3}$-2$\sqrt{3}$=3 | B. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | C. | $\sqrt{3}+2\sqrt{3}$=3 | D. | 3$\sqrt{3}$$÷\sqrt{3}$=3 |
14.某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
下列说法中,不正确的是( )
| 分数(单位:分) | 105 | 130 | 140 | 150 |
| 人数(单位:人) | 2 | 4 | 3 | 1 |
| A. | 这组数据的众数是130 | B. | 这组数据的中位数是130 | ||
| C. | 这组数据的平均数是130 | D. | 这组数据的方差是112.5 |
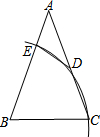 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°.
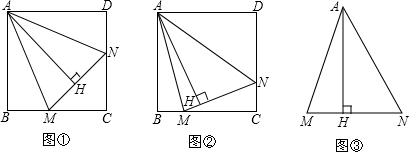
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°. 数学活动课上,四位同学围绕作图问题:“如图,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形,其中作法错误的为( )
数学活动课上,四位同学围绕作图问题:“如图,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形,其中作法错误的为( )