题目内容
7.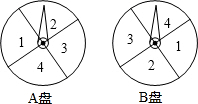 小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).
小明和小亮用如图所示两个转盘(每个转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次,如果两次数字之和为奇数,则小明胜,否则,小亮胜,这个游戏公平吗?答:公平(填“公平”或“不公平”).
分析 先画树状图展示所有16种等可能的结果数,再找出两次数字之和为奇数的结果数和两次数字之和为偶数的结果数,然后计算小明胜的概率和小亮胜的概率,再通过比较两概率的大小判断游戏的公平性.
解答 解:画树状图为:
$\frac{1}{4}$共有16种等可能的结果数,其中两次数字之和为奇数的结果数为8,两次数字之和为偶数的结果数为8,
所以小明胜的概率=$\frac{8}{16}$=$\frac{1}{2}$,小亮胜的概率=$\frac{8}{16}$=$\frac{1}{2}$,
所以这个游戏公平.
故答案为公平.
点评 本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 5$\sqrt{3}$-2$\sqrt{3}$=3 | B. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | C. | $\sqrt{3}+2\sqrt{3}$=3 | D. | 3$\sqrt{3}$$÷\sqrt{3}$=3 |
18.下列几何体中,俯视图为正方形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.政教处王主任将10份奖品分别放在10个完全相同的不透明礼盒中,准备将它们奖给小明等10位获“说题比赛先进个人”称号的同学.这些奖品中有5份是学习文具,3份是数学读本,2份是科技馆通票.小明同学从中随机取一份奖品,恰好取到数学读本的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
19.已知点A(x1,y1),B(x2,y2)均在抛物线y=ax2+2ax-4(0<a<3)上,若x1>x2,x1+x2=1-a,则下列结论中正确的是( )
| A. | y1>y2 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1与y2的大小不确定 |
16.下列运算正确的是( )
| A. | 3x+2x=5x2 | B. | (a+2b)(a-2b)=a2-2b2 | C. | $\sqrt{8}$$-\sqrt{2}$=$\sqrt{6}$ | D. | $\sqrt{(-3)^{2}}$=3 |
17.对于反比例函数y=$\frac{k}{x}$(k≠0),下列说法正确的是( )
| A. | 当k>0时,y随x增大而增大 | |
| B. | 当k<0时,y随x增大而增大 | |
| C. | 当k>0时,该函数图象在二、四象限 | |
| D. | 若点(1,2)在该函数图象上,则点(2,1)也必在该函数图象上 |