题目内容
6.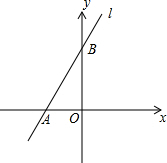 如图,直线l与x轴相交于点A(-2,0),与y轴相交于点B,∠BAO=60°.
如图,直线l与x轴相交于点A(-2,0),与y轴相交于点B,∠BAO=60°.(1)求直线l的解析式;
(2)以点O为圆心,半径为2作圆,判断⊙O与直线l的位置关系;
(3)直接写出△ABO的外接圆圆心O′的坐标.(不必写出过程)
分析 (1)由已知得出OA=2,在Tt△AOB中,由三角函数求出OB=OA•tan60°=2$\sqrt{3}$,得出B(0,2$\sqrt{3}$);设直线l的解析式为y=kx+b,把A(-2,0),B(0,2$\sqrt{3}$)代入得出方程组,解方程组即可;
(2)作OD⊥AB于D,求出∠ABO=30°,由含30°角的直角三角形的性质求出AB=2OA=4,由△AOB的面积=$\frac{1}{2}$AB•OD=$\frac{1}{3}$OA•OB,求出OD=$\sqrt{3}$,得出d<r即可;
(3)由Rt△ABO的外接圆圆心O′为AB的中点,即可得出圆心O′的坐标.
解答 解:(1)∵A(-2,0),
∴OA=2,
在Tt△AOB中,∵∠BAO=60°,
∴OB=OA•tan60°=2×$\sqrt{3}$=2$\sqrt{3}$,
∴B(0,2$\sqrt{3}$);
设直线l的解析式为y=kx+b,
把A(-2,0),B(0,2$\sqrt{3}$)代入得:$\left\{\begin{array}{l}{-2k+b=0}\\{b=2\sqrt{3}}\end{array}\right.$,
解得:k=$\sqrt{3}$,b=2$\sqrt{3}$,
∴直线l的解析式为y=$\sqrt{3}$x+2$\sqrt{3}$;
(2)作OD⊥AB于D,如图所示:
∵∠AOB=90°,∠BAO=60°,
∴∠ABO=30°,
∴AB=2OA=4,
∵△AOB的面积=$\frac{1}{2}$AB•OD=$\frac{1}{3}$OA•OB,
∴OD=$\frac{OA•OB}{AB}$=$\frac{2×2\sqrt{3}}{4}$=$\sqrt{3}$,
∵⊙O的半径r=2>$\sqrt{3}$,即d<r,
∴⊙O与直线l相交;
(3)∵△ABO是直角三角形,OA=2,OB=2$\sqrt{3}$,
∴△ABO的外接圆圆心O′为AB的中点,
∴△ABO的外接圆圆心O′的坐标为(-1,$\sqrt{3}$).
点评 本题是圆的综合题目,考查了待定系数法求直线的解析式、三角函数、勾股定理、含30°角的直角三角形的性质、直角三角形的外接圆等知识;本题综合性强,难度适中,由三角形的面积求出OD是解决问题(2)的关键.

 字词句段篇系列答案
字词句段篇系列答案| A. | 5$\sqrt{3}$-2$\sqrt{3}$=3 | B. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | C. | $\sqrt{3}+2\sqrt{3}$=3 | D. | 3$\sqrt{3}$$÷\sqrt{3}$=3 |
| 分数(单位:分) | 105 | 130 | 140 | 150 |
| 人数(单位:人) | 2 | 4 | 3 | 1 |
| A. | 这组数据的众数是130 | B. | 这组数据的中位数是130 | ||
| C. | 这组数据的平均数是130 | D. | 这组数据的方差是112.5 |
 如图,AB∥CD,AF⊥AB,∠C=120°,则∠EAF的度数为( )
如图,AB∥CD,AF⊥AB,∠C=120°,则∠EAF的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
| A. |  | B. |  | C. |  | D. |  |
| A. | 3x+2x=5x2 | B. | (a+2b)(a-2b)=a2-2b2 | C. | $\sqrt{8}$$-\sqrt{2}$=$\sqrt{6}$ | D. | $\sqrt{(-3)^{2}}$=3 |
 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为( )
如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为( )