题目内容
如图，半径为5的两个等圆⊙O1与⊙O2相交于A、B，公共弦AB=8．由点O1向⊙O2作切线O1C，切点为C，则O1C的长为 ．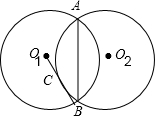
考点：相交两圆的性质,圆与圆的位置关系
专题：常规题型
分析：连接O1O2，O1A，O2C．根据切线的性质定理和勾股定理求解．
解答：
解：连接O1O2，O1A，O2C，
根据两圆的连心线垂直平分两圆的公共弦和勾股定理得O1O2=6；
再根据切线的性质定理和勾股定理得O1C=
=
．
故答案为：
．
解：连接O1O2，O1A，O2C，根据两圆的连心线垂直平分两圆的公共弦和勾股定理得O1O2=6；
再根据切线的性质定理和勾股定理得O1C=
| 62-52 |
| 11 |
故答案为：
| 11 |
点评：本题主要考查相交两圆的性质和圆与圆的位置关系的知识点，此题要综合运用相交两圆的性质、切线的性质定理和勾股定理．
练习册系列答案
口算能手系列答案
相关题目
已知a，b，c为正数，且a≠b，若x=
+
+
，y=
+
+
，则x与y的大小关系是（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| A、x＞y |
| B、x＜y |
| C、x-y |
| D、随a，b，c的取值而变化 |
将一张长方形白纸对折，再沿着与折痕方向平行的方向反复对折，问经过n次后，将纸展开共可得到的折痕条数为（ ）
| A、2n-1 |
| B、2n |
| C、2n-1 |
| D、2n |
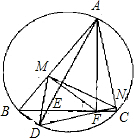如图，在锐角△ABC的BC边上有两点E、F，满足∠BAE=∠CAF，作FM⊥AB，FN⊥AC（M、N是垂足），延长AE交△ABC的外接圆于点D．