题目内容
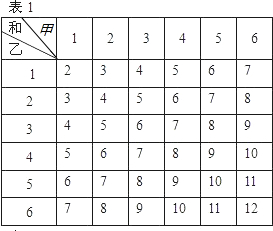
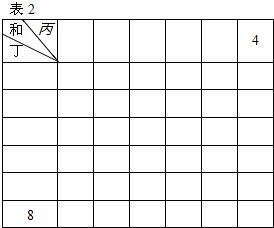
方程组
的解是 .
|
考点:高次方程
专题:计算题
分析:先设u=x+2,v=y+3,把方程组化简为
,然后再设u+v=s,uv=t,利用完全平方公式化简后,再用加减消元可以求出方程组的解.
|
解答:解:设x+2=u,y+3=v,则原方程组变为
又设u+v=s,uv=t,则原方程组又变形为:
由(2)除以(1)得s-
=19(3)
由(1)(3)得
∴
解之得
或
∴
或
∴原方程组之解为
|
|
由(2)除以(1)得s-
| t |
由(1)(3)得
|
∴
|
|
|
∴
|
|
∴原方程组之解为
|
|
点评:本题考查的是高次方程组,利用换元的方法把方程化简降次,然后用加减消元法可以求出方程组的解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
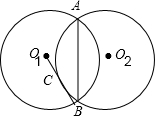
 已知△ABC中,O为外心,I为内心,且AB+AC=2BC.求证:OI⊥AI(图).
已知△ABC中,O为外心,I为内心,且AB+AC=2BC.求证:OI⊥AI(图).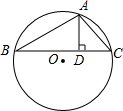 如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=
如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=