题目内容
已知p、q均为质数,且满足5p2+3q=59,则p+q= .
考点:质数与合数
专题:探究型
分析:先根据5p2+3q=59可知,p、q中必为一奇一偶,再根据p、q均为质数可知,p、q中必有一数为2,再根据p=2或q=2求出另一未知数的对应知,找出符合条件的对应值代入所求代数式即可.
解答:解:∵5p2+3q=59,
∴p、q中必为一奇一偶,
∵p、q均为质数,
∴p、q中必有一数为2,
假设q=2,则p2=
,不合题意,
∴p=2,q=
=13,
∴p+q=15.
故答案为:15.
∴p、q中必为一奇一偶,
∵p、q均为质数,
∴p、q中必有一数为2,
假设q=2,则p2=
| 53 |
| 5 |
∴p=2,q=
| 59-20 |
| 3 |
∴p+q=15.
故答案为:15.
点评:本题考查的是质数与合数、奇数与偶数,解答此题的关键是熟知在所有偶数中只有2是质数这一关键知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
Given p,q are real numbers,and p+2q=0(q≠0),then the value of |
-1|+|
-2|+||
|-3| is( )
| p |
| |q| |
| |p| |
| q |
| p |
| q |
| A、4 | B、6 | C、3 | D、4 or 6 |
将a千克含盐10%的盐水配制成含盐15%的盐水,需加盐x千克,则由此可列出方程为( )
| A、a(1-10%)=(a+x)(1-15%) |
| B、a×10%=(a+x)×15% |
| C、a×10%+x=a×15% |
| D、a(1-10%)=x(1-15%) |
某工厂去年的生产总值比前年增长了P%,那么,前年的生产总值比去年减少的百分数是( )
| A、P% | ||
B、
| ||
C、
| ||
D、(1+
|
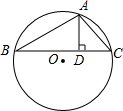 如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=
如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=