题目内容
12.二次函数y=kx2-2x+1的图象与x轴有两个交点,则k的取值范围是( )| A. | k<1 | B. | k<1且k≠0 | C. | k≤1 | D. | k≤1且k≠0 |
分析 根据二次函数y=kx2-2x+1的图象与x轴有两交点,可知kx2-2x+1=0时的△>0,且k≠0,从而可以求得k的取值范围.
解答 解:∵二次函数y=kx2-2x+1的图象与x轴有交点,
∴kx2-2x+1=0时,
$\left\{\begin{array}{l}{(-2)^{2}-4×k×1>0}\\{k≠0}\end{array}\right.$,
解得k<1且k≠0.
故选B.
点评 本题考查二次函数与x轴的交点,能将抛物线与一元二次方程建立关系以及注意二次项系数不等于0是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
20.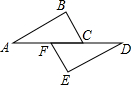 如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
 如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )
如图,在△ABC和△DEF中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件( )| A. | ∠A=∠D | B. | AB=FD | C. | AC=ED | D. | AF=CD |
7.若等边三角形ABC内接于⊙O,点P在$\widehat{CAB}$上(P不与B、C重合),则∠BPC等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
1.一个多边形截去一个角(截线不过顶点)之后,所形成的多边形的内角和是2520°,那么原多边形的边数是( )
| A. | 19 | B. | 17 | C. | 15 | D. | 13 |
 如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.若AB=2$\sqrt{3}$,∠AB′D=75°,则BC=$3+\sqrt{3}$.
如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连结B′D.若AB=2$\sqrt{3}$,∠AB′D=75°,则BC=$3+\sqrt{3}$. 如图,若∠AOC=∠BOD,且∠AOC=70°,∠BOC=50°,则∠COD=20°.
如图,若∠AOC=∠BOD,且∠AOC=70°,∠BOC=50°,则∠COD=20°.