题目内容
17.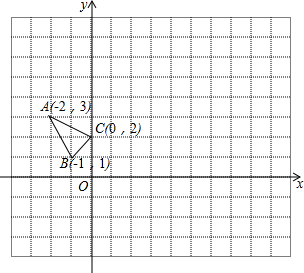 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.(1)将△ABC沿x轴翻折得到△A1B1C1,作出△A1B1C1;
(2)将△A1B1C1向右平移3个单位后得△A2B2C2,作出△A2B2C2.
(3)在x轴上找一点P,使PA1+PC2的值最小,则点P的坐标为(1,0).(不写解答过程,直接写出结果)
分析 (1)首先确定A、B、C关于x轴对称的点的位置A1、B1、C1,再连接即可;
(2)首先确定A1、B1、C1向右平移3个单位后对应点的位置,再连接即可;
(3)当P在x轴上,PA1+PC2的值最小,需要确定A1关于x轴的对称点位置,即为A点位置,连接AB2,与x轴的交点就是P的位置.
解答 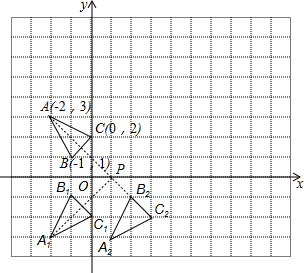 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)连接AB2,与x轴的交点就是P的位置,
设直线AC2的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=3}\\{3k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
故直线AC2的解析式为:y=-x+1,
当y=0时,x=1,
故P点坐标为(1,0).
点评 此题主要考查了作图--轴对称变换和平移,以及最短路线,关键是掌握在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.

练习册系列答案
相关题目
7.若等边三角形ABC内接于⊙O,点P在$\widehat{CAB}$上(P不与B、C重合),则∠BPC等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
12.关于二次函数$y=-\frac{1}{2}{(x-1)^2}+2$的图象与性质,下列结论错误的是( )
| A. | 抛物线与x轴有两个交点 | B. | 当x=1时,函数有最大值 | ||
| C. | 抛物线可由$y=-\frac{1}{2}{x^2}$经过平移得到 | D. | 当-1<x≤2时,函数y的整数值有3个 |
 如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点.
如图,一次函数y=-2x+8与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A,B两点,且A(1,0)抛物线的对称轴是x=-$\frac{3}{2}$.
如图,一次函数y1=kx+1与二次函数y2=ax2+bx-2交于A,B两点,且A(1,0)抛物线的对称轴是x=-$\frac{3}{2}$.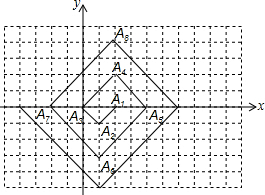 如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).
如图,在一单位长度为1的方格纸上.△A1A2A3,△A3A4A5,△A5A6A7…都是斜边在x轴上,斜边长分别为2,4,6…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0).则依图中所示规律,A2016的坐标是(2,1008).