题目内容
13.计算:(1)($\frac{1}{4}$+$\frac{1}{6}$-$\frac{1}{2}$)×(-12)
(2)-14+(-2)÷(-$\frac{1}{3}$)+|-9|
(3)2a2b-5ab2-3ba2+7b2a
(4)(5a2+2a-1)-4(2a2-8a+3)
分析 (1)利用乘法分配律计算即可;
(2)先算乘方与绝对值,再算乘除,最后算加减;
(3)直接合并同类项即可;
(4)先去括号,然后合并同类项即可.
解答 解:(1)($\frac{1}{4}$+$\frac{1}{6}$-$\frac{1}{2}$)×(-12)=-3-2+6=1;
(2)-14+(-2)÷(-$\frac{1}{3}$)+|-9|=-1+6+9=14;
(3)2a2b-5ab2-3ba2+7b2a=-a2b+2ab2;
(4)(5a2+2a-1)-4(2a2-8a+3)
=5a2+2a-1-8a2+32a-12
=-3a2+34a-13.
点评 本题考查了整式的加减,整式的加减的实质就是去括号、合并同类项.一般步骤是:先去括号,然后合并同类项.去括号时,要注意两个方面:一是括号外的数字因数要乘括号内的每一项;二是当括号外是“-”时,去括号后括号内的各项都要改变符号.也考查了有理数的混合运算.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
1.已知关于x的分式方程$\frac{a+2}{x+1}$=1的解是非正数,则a的取值范围是( )
| A. | a≤-1 | B. | a≤1且a≠-2 | C. | a≤-1且a≠-2 | D. | a≤1 |
18.已知方程x2k-1+3=0是关于x的一元一次方程,则k的值等于( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.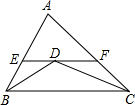 如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
 如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
如图,△ABC中,BD,CD分别平分∠ABC,∠ACB,过点D作EF∥BC交AB,AC于点E,F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )| A. | EF>BE+CF | B. | EF=BE+CF | C. | EF<BE+CF | D. | 不能确定 |
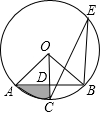 如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)
如图,点A、B、E在⊙O上,半径OC⊥AB于点D,∠CEB=22.5°,OD=$\sqrt{2}$,则图中阴影部分的面积等于$\frac{1}{2}π$-1.(结果保留π)