题目内容
3．已知关于x的一元二次方程x2+（m+3）x-1=0．（1）求证：无论m取何值，原方程总有两个不相等的实数根；
（2）若此方程有一个根为1，求m的值．
分析 （1）先把方程化为一般式，找出a，b和c，求出根的判别式进行解答；
（2）先把x=-1代入原方程求出m的值．
解答 证明：（1）∵△=b2-4ac=（m+3）2+4＞0，
∴无论m取何值，原方程总有两个不相等的实数根；
（2）把x=1代入得：1+（m+3）×1-1=0，
解得m=-3．
点评 本题主要考查了根的判别式以及一元二次方程的解的知识，解答本题的关键是掌握根的判别式△＞0?方程有两个不相等的实数根，此题难度不大．
练习册系列答案
相关题目
11．
如图，在⊙O中，∠BOC=100°，则∠A等于（ ）
如图，在⊙O中，∠BOC=100°，则∠A等于（ ）| A． | 100° | B． | 25° | C． | 40° | D． | 50° |
8．在-1，0，$\frac{1}{3}$，$\sqrt{2}$，π，0.10110中任取一个数是无理数的概率（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
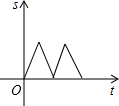
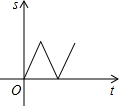
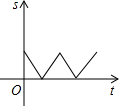
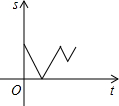
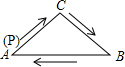如图，在△ABC中，AC=BC，有一动点P从A出发，沿A→C→B→A匀速运动．设点P的运动时间为t，CP的长度s，则s与t之间的函数关系用图象描述大致是（ ）
