题目内容
14.已知,函数y=(m+1)x2-(m-4)x+(m-5)的图象过点A(-6,7).(1)求此函数的关系式;
(2)求该函数图象与x轴的两个交点B、C与顶点P所围成的△BPC面积是27;
(3)观察函数图象,指出当-3<x<1时y的取值范围是-9≤y<0.
(4)若A(m-1,y1),B(m+1,y2)两点都在该二次函数的图象上,试比较y1与y2的大小.
分析 (1)将点A(-6,7)代入y=(m+1)x2-(m-4)x+(m-5),得到关于m的方程,解方程求出m的值即可;
(2)根据(1)中所求解析式,求出B、C、P的坐标,再根据三角形的面积公式即可求出△BPC的面积;
(3)由顶点P的横坐标为-2,可得-3<x<1时y的最小值是顶点纵坐标的值,再根据二次函数的性质求出最大值即可求解;
(4)先将(1)中所求m的值代入得出A、B两点的坐标,再根据二次函数的性质即可求解.
解答 解:(1)∵函数y=(m+1)x2-(m-4)x+(m-5)的图象过点A(-6,7),
∴7=(m+1)×(-6)2-(m-4)×(-6)+(m-5),
解得m=0,
则此函数的关系式为y=x2+4x-5;
(2)∵y=x2+4x-5,
∴y=0时,x2+4x-5=0,
解得x=-5或1,
∴该函数图象与x轴的两个交点B、C的坐标为(-5,0),(1,0).
∵y=x2+4x-5=(x+2)2-9,
∴顶点P的坐标是(-2,-9),
∴△BPC的面积是:$\frac{1}{2}$×6×9=27;
(3)∵y=x2+4x-5=(x+2)2-9,
∴对称轴是x=-2,
∴当-3<x<1时,y的最小值是-9,
当x=1时,y的最大值是(1+2)2-9=0,
∴当-3<x<1时y的取值范围是-9≤y<0;
(4)∵m=0,
∴A(-1,y1),B(1,y2),
∵y=x2+4x-5的对称轴是x=-2,抛物线开口向上,
∴当x>-2时,y随x的增大而增大,
∵-2<-1<1,
∴y1<y2.
故答案为27;-9≤y<0.
点评 本题考查了待定系数法求二次函数的解析式,二次函数图象上点的坐标特征,二次函数的性质,正确求出函数的解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.代数式-$\frac{π}{7}$αb2的系数是( )
| A. | -7 | B. | -π | C. | -$\frac{π}{7}$ | D. | -$\frac{1}{7}$ |
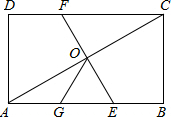 如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )
如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( ) 如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为40度.
如图,△ABC∽△ACP,若∠A=75°,∠APC=65°,则∠B的大小为40度.