题目内容
9.已知等腰三角形的一个内角为50°,则底角为65或50度.若一个等腰三角形的两边长分别是2cm和5cm,则它的周长是12 cm;若一个等腰三角形中,已知两边的长分别是9和5,则周长为19或23.分析 ①由等腰三角形的一个内角为50°,可分别从50°的角为底角与50°的角为顶角去分析求解,即可求得答案;②本题没有明确说明已知的边长那一条是腰长,所以需要分两种情况讨论;③分9是底和腰两种情况进行讨论,利用三角形的三边关系来判断,再计算其周长即可.
解答 解:①∵等腰三角形的一个内角为50°,
若这个角为顶角,则底角为:$\frac{180°-50°}{2}$=65°,
若这个角为底角,则另一个底角也为50°,
∴其一个底角的度数是65°或50°,
故答案为:65°或50°;
②分两种情况讨论
腰长为5时,三边为5、5、2,满足三角形的性质,周长=5+5+2=12cm;
腰长为2cm时,三边为5、2、2,
∵2+2=4<5,
∴不满足构成三角形,
∴周长为12cm,
故答案为:12;
③当边长为9的边为底时,三角形的三边长为:9、5、5,满足三角形的三边关系,此时其周长为19;
当边长为9的边为腰时,三角形的三边长为:9、9、5,满足三角形的三边关系,此时其周长为23.
故答案为:19或23.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
20.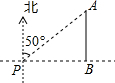 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
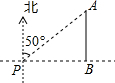 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )| A. | 10海里 | B. | 10sin50°海里 | C. | 10cos50°海里 | D. | 10tan50°海里 |
17.一个矩形的周长为30,若矩形的一边长用字母x表示,则此矩形的面积为( )
| A. | x(15-x) | B. | x(30-x) | C. | x(30-2x) | D. | x(15+x) |
19.下列说法错误的是( )
| A. | 所有有理数都可用数轴上的点表示 | |
| B. | 数轴上原点表示的数是0 | |
| C. | 数轴上表示-3的点与表示+3的点的距离是3 | |
| D. | 最大的负整数是-1 |
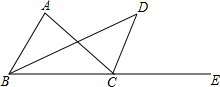 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D; 如图,在平面直角坐标系xOy中,点A1,A2,A3,…都在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…,都是等腰直角三角形,如果OA1=1,则点B2015的坐标是
如图,在平面直角坐标系xOy中,点A1,A2,A3,…都在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…,都是等腰直角三角形,如果OA1=1,则点B2015的坐标是