题目内容
2．
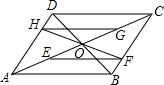如图，?ABCD的两条对角线AC、BD相交于点O，E、G分别是OA、OC的中点，过点O作任一条直线交AD于点H，交BC于点F，猜想EF与HG的关系，并证明你的猜想．
分析 此题给出了四边形的对角线，所以可以采用对角线互相平分的四边形是平行四边形证得．首先根据已知证得△AOE≌△COF，则可证得OE=OF；又因为四边形ABCD是平行四边形，G是OC的中点，E是OA的中点，所以可以证得OF=OH，所以四边形EFGH是平行四边形．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，OA=OC，
∴∠ODH=∠OBF，∠OHD=∠OFB，
在△OHD与△OFB中，$\left\{\begin{array}{l}{∠ODH=∠OBF}\\{∠OHD=∠OFB}\\{OD=OB}\end{array}\right.$，
∴△OHD≌△OFB，
∴OH=OF，
∵E是OA的中点，G是OC的中点，
∴OE=$\frac{1}{2}$OA，OG=$\frac{1}{2}$OC，
∴OG=OE，
∴四边形EFGH是平行四边形，
∴EF=GH．
点评 本题考查了平行四边形的判定与性质．解题的关键是选择适宜的证明方法．此题出现了对角线，所以选择对角线互相平分的四边形是平行四边形证明比较简单．
练习册系列答案
科学实验活动册系列答案
相关题目
如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根铁棒的$\frac{1}{3}$露出水面，另一根铁棒的$\frac{1}{4}$露出水面．两根铁棒长度之和为34cm，此时木桶中水的深度是12cm．
已知：（-4，-1），（-2，0），（-1，4），（0，-5），（0，0），（0，1），（1，4），（2，2），（3，0），（4，1），（4，3），（6，4）．将这12个点按要求进行不同的分类：