题目内容
13. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根铁棒的$\frac{1}{3}$露出水面,另一根铁棒的$\frac{1}{4}$露出水面.两根铁棒长度之和为34cm,此时木桶中水的深度是12cm.
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根铁棒的$\frac{1}{3}$露出水面,另一根铁棒的$\frac{1}{4}$露出水面.两根铁棒长度之和为34cm,此时木桶中水的深度是12cm.
分析 设较长铁棒的长度为xcm,较短铁棒的长度为ycm.因为两根铁棒之和为34cm,故可的方程:x+y=34,又知两棒未露出水面的长度相等,又可得方程$\frac{2}{3}$x=$\frac{3}{4}$y,把两个方程联立,组成方程组,解方程组可得较长的铁棒的长度,用较长的铁棒的长度×$\frac{2}{3}$可以求出木桶中水的深度.
解答 解:设较长铁棒的长度为xcm,较短铁棒的长度为ycm,由题意得:
$\left\{\begin{array}{l}{x+y=34}\\{\frac{2}{3}x=\frac{3}{4}y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=18}\\{y=16}\end{array}\right.$,
因此木桶中水的深度为18×$\frac{2}{3}$=12(cm),
故答案为:12.
点评 此题主要考查了二元一次方程组的应用,关键是弄清题意,找出合适的等量关系,列出方程组.

练习册系列答案
相关题目
3.-(-1)2014的运算结果是( )
| A. | -1 | B. | 1 | C. | 2014 | D. | -2014 |
1.在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是( )
| A. | 随着抛掷次数的增加,正面向上的频率越来越小 | |
| B. | 当抛掷的次数n很大时,正面向上的次数一定为$\frac{n}{2}$ | |
| C. | 不同次数的试验,正面向上的频率可能会不相同 | |
| D. | 连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率小于$\frac{1}{2}$ |




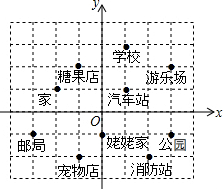 下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.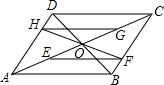 如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想.
如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想. 如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).
如图,梯形OABC中,CB∥OA,O为坐标原点,B(2,4),C(0,4),tan∠BAO=2,动点Q 从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点Q作OP⊥x轴交折线C-B-A于点P,以PQ为一边向左作正方形PQRS,设运动时间为t (秒),正方形PQRS与梯形OABC重叠的面积为S(平方单位).