题目内容
14. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.(1)求a,b的值;
(2)求直线AB′与抛物线的对称轴的交点C的坐标.
分析 (1)先求出B(0,3),由平移的性质得出B′(2,3),用待定系数法求出a,b即可;
(2)设直线AB′的解析式为y=kx+n,用待定系数法求出求出直线AB′的解析式,再求出抛物线的对称轴,即可求出点C的坐标为(1,2).
解答 解:(1)当x=0时,y=3,
∴B(0,3),
∵点B沿x轴的正方向平行移动2个单位长度,得到点B′,
∴B′(2,3),
把点A(-1,0),B′(2,3)代入抛物线y=ax2+bx+3得:$\left\{\begin{array}{l}{a-b+3=0}\\{4a+2b+3=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
即a=-1,b=2;
(2)设直线AB′的解析式为y=kx+n,
把点A(-1,0),B′(2,3)代入得:$\left\{\begin{array}{l}{-k+n=0}\\{2k+n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{n=1}\end{array}\right.$,
∴直线AB′的解析式为y=x+1,
∵抛物线y=-x2+2x+3的对称轴是直线x=-$\frac{2}{2×(-1)}$=1,
∴当x=1时,y=2,
∴点C的坐标为(1,2).
点评 本题考查了抛物线与x轴的交点、平移的性质、待定系数法求抛物线和直线的解析式、对称轴的求法;熟练掌握待定系数法求抛物线和直线的解析式是解决问题的关键.

练习册系列答案
相关题目
4.给出下列3个结论:
①边长相等的多边形内角都相等;
②对角线互相垂直的平行四边形是菱形;
③圆心到直线的距离恰好等于圆的半径,则该直线是圆的切线.
其中正确结论的个数有( )
①边长相等的多边形内角都相等;
②对角线互相垂直的平行四边形是菱形;
③圆心到直线的距离恰好等于圆的半径,则该直线是圆的切线.
其中正确结论的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
5.点P在第二象限,且到x轴的距离为5,到y轴的距离为3,则点P的坐标是( )
| A. | (-5,3) | B. | (3,-5) | C. | (-3,5) | D. | (5,-3) |
2.线段AB是由线段PQ平移得到的,点P(-1,3)的对应点为A(4,7),则点Q(-3,1)的对应点B的坐标是( )
| A. | (2,5) | B. | (-6,-1) | C. | (-8,-3) | D. | (-2,-2) |
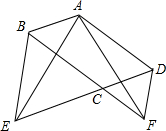 如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF.
如图,在平行四边形ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,使得△BCE和△CDF都是正三角形.求证:AE=AF.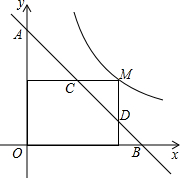 如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4. 如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E、F、G、H分别在AD、AB、BC、CD上的点,且AE=BF=CG=DH,分别将△AEF、△BFG、△CGH、△DHE沿EF、FG、GH、HE翻折,得四边形MNKP,设AE=x,S四边形MNKP=y,则y关于x的函数图象大致为( )



 如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A、B、C、D的边长分别是12,16,9,12,则最大正方形E的面积是625.
如图,图中所有的四边形都是正方形,所有的三角形都是直角三角形,已知正方形A、B、C、D的边长分别是12,16,9,12,则最大正方形E的面积是625.