题目内容
2.线段AB是由线段PQ平移得到的,点P(-1,3)的对应点为A(4,7),则点Q(-3,1)的对应点B的坐标是( )| A. | (2,5) | B. | (-6,-1) | C. | (-8,-3) | D. | (-2,-2) |
分析 先根据点P、A的坐标判断平移的方向与距离,再根据点Q的坐标计算出点B的坐标即可.
解答 解:∵点P(-1,3)的对应点为A(4,7),
∴线段向右平移的距离为:4-(-1)=5,向上平移的距离为:7-3=4,
∴点Q(-3,1)的对应点B的横坐标为:-3+5=2,纵坐标为:1+4=5,
∴B(2,5).
故选(A)
点评 本题主要考查了坐标与图形变化,掌握坐标的平移变化规律是解题的关键.在坐标平面内,左右平移时,点的横坐标改变;上下平移时,点的纵坐标改变.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
12.抛物线y=ax2+bx+c的图象只经过第一、二象限,那么关于△=b2-4ac,下列结论成立的是( )
| A. | △<0 | B. | △≤0 | C. | △>0 | D. | △≥0 |
10. 如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
 如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )
如图,已知一条直线经过点A(0,2),点B(1,0),将这条直线向左平移与x轴、y轴分别交于点C、点D,若DB=DC,则直线CD的函数解析式为( )| A. | y=-x+2 | B. | y=-2x-2 | C. | y=2x+2 | D. | y=-2x+2 |
17.在平面直角坐标系中,点A(-4,0),点B(2,0),若点C在一次函数y=-$\frac{1}{2}x+2$的图象上,且△ABC为直角三角形,则满足条件的点C有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.二次函数y=x2的图象是( )
| A. | 线段 | B. | 直线 | C. | 抛物线 | D. | 双曲线 |
 如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( )
如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( )



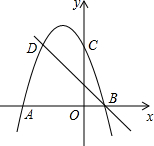 如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D.
如图,二次函数的图象与x轴交于点A(-3,0),B(1,0),交y轴于点C(0,3),点C,D是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点B,D. 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上. 如图所示的图形为中心对称图形,点O为它的对称中心,写出一组关于点O的对称点是点A与点C.
如图所示的图形为中心对称图形,点O为它的对称中心,写出一组关于点O的对称点是点A与点C.