题目内容
6.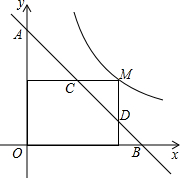 如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.
如图,M为双曲线y=$\frac{2}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD•BC的值为4.
分析 作CE⊥x轴于E,DF⊥y轴于F,如图,对于直线y=-x+m,分别令x与y为0求出对应y与x的值,表示出A与B坐标,进而得到三角形AOB为等腰直角三角形,确定出三角形ADF与三角形CEB为等腰直角三角形,设M(a,b),代入反比例解析式求出ab的值,表示出CE与DF长,进而表示出AD与BC的长,即可求出AD•BC的值.
解答 解:作CE⊥x轴于E,DF⊥y轴于F,如图,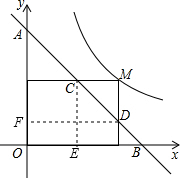 对于y=-x+m,
对于y=-x+m,
令x=0,则y=m;令y=0,-x+m=0,解得x=m,
∴A(0,m),B(m,0),
∴△OAB等腰直角三角形,
∴△ADF和△CEB都是等腰直角三角形,
设M的坐标为(a,b),则ab=2,CE=b,DF=a,
∴AD=$\sqrt{2}$DF=$\sqrt{2}$a,BC=$\sqrt{2}$CE=$\sqrt{2}$b,
∴AD•BC=$\sqrt{2}$a•$\sqrt{2}$b=2ab=4.
故答案为:4.
点评 此题属于反比例函数综合题,涉及的知识有:一次函数与坐标轴的交点,等腰直角三角形的判定与性质,以及反比例函数的性质,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
17.在平面直角坐标系中,点A(-4,0),点B(2,0),若点C在一次函数y=-$\frac{1}{2}x+2$的图象上,且△ABC为直角三角形,则满足条件的点C有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.二次函数y=x2的图象是( )
| A. | 线段 | B. | 直线 | C. | 抛物线 | D. | 双曲线 |
15.下面四个几何体中,主视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.