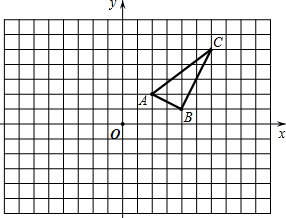
题目内容
9.已知M(a,3)和N(4,b)关于x轴对称,则(a+b)2012的值为1.分析 直接利用关于x轴对称点的性质得出a,b的值,进而求出答案.
解答 解:∵M(a,3)和N(4,b)关于x轴对称,
∴a=4,b=-3,
∴(a+b)2012=(4-3)2012=1.
故答案为:1.
点评 此题主要考查了关于x轴对称点的性质,正确得出a,b的值是解题关键.

练习册系列答案
相关题目
19.已知二次函数y=-x2+bx+c中,函数y与自变量x之间的部分对应值如表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,则有( )
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1<y2 | ||
| C. | y1=y2 | D. | y1与y2大小无法确定 |
17.在平面直角坐标系中,点A(-4,0),点B(2,0),若点C在一次函数y=-$\frac{1}{2}x+2$的图象上,且△ABC为直角三角形,则满足条件的点C有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
4.已知A(x1,y1)、B(x2,y2)和C(x3,y3)在直线y=-$\frac{1}{2}$x+$\sqrt{3}$上.若x1<x2<x3,下列判断正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
19.在Rt△ABC中,∠B=90°,∠C=30°,AC=2,则AB的长为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
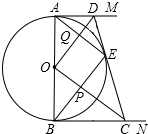 如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论: 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的一个交点A的坐标是(-1,0),与y轴相交于点B,将点B沿x轴的正方向平行移动2个单位长度,得到点B′,点B′恰好落在抛物线上.