题目内容
9.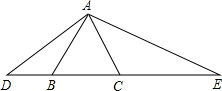 如图,△ABC是等边三角形,∠DAE=120°.求证:
如图,△ABC是等边三角形,∠DAE=120°.求证:(1)AD•AE=AB•DE;
(2)BC2=DB•CE.
分析 (1)根据已知条件得到∠DAB+∠CAE=60°,根据外角的性质得到∠CAE+∠E=∠ACB=60°,求得∠DAB=∠E,根据邻补角的定义得到∠ABD=∠ACE=120°,推出△ABD∽△ADE,根据相似三角形的性质得到$\frac{AD}{DE}=\frac{AB}{AE}$,即可得到结论;
(2)根据(1)的结论证得△ABD∽△ECA可知$\frac{AB}{CE}=\frac{BD}{AC}$,即AB•AC=BD•CE,故可得出结论.
解答 证明:(1)∵△ABC是等边三角形,∠DAE=120°,
∴∠DAB+∠CAE=60°,
∵∠ACB是△ACE的外角,
∴∠CAE+∠E=∠ACB=60°,
∴∠DAB=∠E,
∵∠ABC=∠ACB=60°,
∴∠ABD=∠ACE=120°,
∴△ABD∽△ADE,
∴$\frac{AD}{DE}=\frac{AB}{AE}$,
∴AD•AE=AB•DE;
(2)∵∠DAB=∠E,∠ABC=∠ACE=120°,
∴△ABD∽△AEC,
∴$\frac{AB}{CE}=\frac{BD}{AC}$,
即AB•AC=BD•CE,
∵AB=AC=BC,
∴BC2=BD•CE.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,熟记等边三角形的性质是解题的关键.

练习册系列答案
相关题目
14.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,则下列关系式中:①a=c•sinA ②b=a•tanB ③a=b•tanA ④b=c•cosB ⑤c=$\frac{b}{sinB}$ ⑥c=$\frac{a}{cosA}$ 错误的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.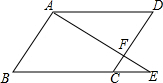 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 3:1 |
18.小明把自己某学期的期中、期末数学考试成绩按2:3的权重比例来算,算出的学期总评成绩为86分,数学老师按如下的规定算出的却是84分.规定:?学生的平时成绩、期中考试、期末考试三项成绩分别按30%,30%,40%的比例计入学期总评成绩;?学生的平时成绩按各单元考试所有成绩的中位数确定.
已知小明各单元考试的成绩如下表:
(1)求出小明各单元考试成绩的中位数、众数;
(2)小明期中、期末考试的数学成绩分别是多少?
已知小明各单元考试的成绩如下表:
| 单元编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
| 测试分数 (分) | 85 | 76 | 75 | 84 | 85 | 74 | 75 | 88 |
(2)小明期中、期末考试的数学成绩分别是多少?
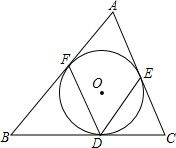 如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.