题目内容
16.解分式方程:$\frac{1}{{x}^{2}+3x+2}$+$\frac{{x}^{2}}{{x}^{2}-4}$=$\frac{3}{{x}^{2}-x-2}$+1.分析 分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:已知方程整理得:$\frac{1}{(x+1)(x+2)}$+$\frac{{x}^{2}}{(x+2)(x-2)}$=$\frac{3}{(x-2)(x+1)}$+1,
去分母得:x-2+x2(x+1)=3(x+2)+(x+1)(x+2)(x-2),
去括号得:x-2+x3+x2=3x+6+x3-4x+x-4,即x2+x-4=0,
解得:x=$\frac{-1±\sqrt{17}}{2}$,
经检验x=$\frac{-1+\sqrt{17}}{2}$与x=$\frac{-1-\sqrt{17}}{2}$都是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
1.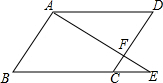 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 3:1 |
2.张明同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近一棵树的影长为8米,则这棵树的高是( )米.
| A. | 10 | B. | 6.4 | C. | 4 | D. | 无法确定 |
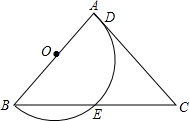 如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.
如图,△ABC中,AB=AC,∠A=80°,以AB为直径的半圆交AC于D,交BC于E,求$\widehat{AD}$、$\widehat{DE}$、$\widehat{BE}$所对圆心角的度数.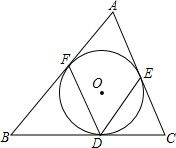 如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.