题目内容
16.在Rt△ABC中,已知∠B=90°,AC=10,AB=5$\sqrt{2}$,则∠A等于( )| A. | 45° | B. | 30° | C. | 60° | D. | 50° |
分析 根据勾股定理求出BC的长度,然后求出∠A的度数.
解答 解:在Rt△ABC中,
∵∠B=90°,AC=10,AB=5$\sqrt{2}$,
∴BC=$\sqrt{1{0}^{2}-(5\sqrt{2})^{2}}$=5$\sqrt{2}$,
即AB=BC,
∴∠A=45°.
故选A.
点评 本题考查了特殊角的三角函数值,解答本题的关键是根据勾股定理求出BC的长度.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
1.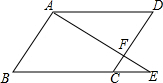 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
 如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )
如图,点F为?ABCD边CD上一点,且CF:FD=1:2,连接AF并延长交BC边的延长线于点E,则CE:BC等于( )| A. | 1:2 | B. | 2:1 | C. | 1:3 | D. | 3:1 |
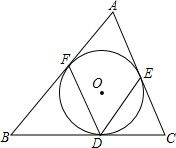 如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.
如图,△ABC内,内切圆⊙O与BC,AC,AB分别相切于点D,E,F,若∠FDE=65°,求∠A的度数.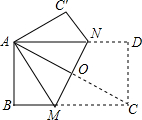 如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.
如图,在矩形ABCD中,AD>AB,点M,N分别在BC,AD边上,将矩形ABCD以直线MN为折痕进行折叠,翻折后能使点C恰好与A点重合,△AMN是一个怎样的三角形?请说明理由.