题目内容
3.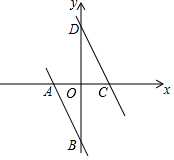 如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )
如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )| A. | y=-2x+2 | B. | y=2x-2 | C. | y=-x-2 | D. | y=-2x-2 |
分析 设直线AB的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答,根据平行直线的解析式的k值相等设出直线CD的表达式,再根据平行四边形的性质求出点C的坐标,然后代入求解即可.
解答 解:设直线AB的解析式为y=kx+b,
∵直线经过点A(-1,0),B(0,-2)
∴$\left\{\begin{array}{l}{b=-2}\\{-k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
∴直线AB的解析式为y=-2x-2;
(2)∵CD为直线AB向上平移得到,
∴设直线CD的解析式为y=-2x+c,
∵AB=DC,AB∥CD,
∴四边形ABCD是平行四边形,
∴OD=OB,
∴点C的坐标为(0,2),
∴c=2,
∴直线CD的解析式为y=-2x+2.
故选A.
点评 本题考查了一次函数图象与几何变换,待定系数法求一次函数解析式,平行四边形的判定和性质,难点在于利用平行直线的解析式的k值相等设出直线CD的表达式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
14.如图,BF、CF分别是∠DBC和∠ECB的角平分线,则关于F的说法不正确的是( )
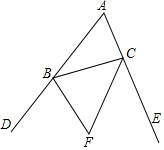

| A. | F到△ABC三边所在直线的距离相等 | B. | F在∠A的平分线上 | ||
| C. | F到△ABC三顶点的距离相等 | D. | F到BD、CE的距离相等 |
18. 将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
 将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )
将x张长为30厘米、宽为10厘米的长方形白纸按如图所示的方法粘合起来,粘合部分的宽度为2厘米,粘合后的总长度为y厘米,则y关于x的函数关系式是( )| A. | y=30x | B. | y=28x | C. | y=28x-2 | D. | y=28x+2 |
 如图,平面直角坐标系中,点A坐标为(1,0),点B绕点A顺时针旋转90°得点B’的坐标为(2,3),则B的坐标为(-2,1).
如图,平面直角坐标系中,点A坐标为(1,0),点B绕点A顺时针旋转90°得点B’的坐标为(2,3),则B的坐标为(-2,1).