题目内容
12. 如图,平面直角坐标系中,点A坐标为(1,0),点B绕点A顺时针旋转90°得点B’的坐标为(2,3),则B的坐标为(-2,1).
如图,平面直角坐标系中,点A坐标为(1,0),点B绕点A顺时针旋转90°得点B’的坐标为(2,3),则B的坐标为(-2,1).
分析 首先过点B′作B′C⊥x轴于点C,过点B作BD⊥x轴于点D,进而得出△ABD≌△B′AC(AAS),即可得出B的坐标.
解答  解:过点B′作B′C⊥x轴于点C,过点B作BD⊥x轴于点D,
解:过点B′作B′C⊥x轴于点C,过点B作BD⊥x轴于点D,
∵点A坐标为(1,0),B’的坐标为(2,3),
∴AC=2-1=1,B′C=3,
∵点B绕点A顺时针旋转90°得点B’,
∴∠BAB′=90°,
∴∠DOB+∠CAB′=90°,
∵∠CAB′+∠AB′C=90°,
∴∠DAB=∠AB′C,
在△ABD和△B′AC中,
$\left\{\begin{array}{l}{∠BDA=∠ACB′}\\{∠DAB=∠B′}\\{AB=AB′}\end{array}\right.$,
∴△ABD≌△B′AC(AAS),
∴BD=AC=1,AD=B′C=3,
∴DO=3-1=2,
∴则B的坐标为:(-2,1).
故答案为:(-2,1).
点评 此题主要考查了坐标与图形的性质和全等三角形的判定与性质,正确利用旋转的性质得出△ABD≌△B′AC是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.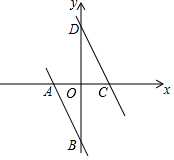 如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )
如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )
 如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )
如图,一条直线经过A(-1,0),B(0,-2)两点,将这条直线向上平移后,与x轴,y轴的交点分别为C,D.若AB=CD,则直线CD的函数关系表达式为( )| A. | y=-2x+2 | B. | y=2x-2 | C. | y=-x-2 | D. | y=-2x-2 |
20.南海总面积约为3500000平方公里,3500000用科学记数法表示应为( )
| A. | 0.35×108 | B. | 3.5×106 | C. | 3.5×107 | D. | 35×105 |
1.如果方程$\left\{\begin{array}{l}{x=y+5}\\{2x-y=5}\end{array}\right.$的解满足方程x+y+a=0,那么a的值是( )
| A. | -5 | B. | 5 | C. | -3 | D. | 3 |
2.2017年春运期间,全国水运旅客发送量约为43500000人次,将43500000用科学记数法表示应为( )
| A. | 0.435×107 | B. | 43.5×106 | C. | 43.5×107 | D. | 4.35×107 |



